
【题目】某超市销售一种成本为每台20元的台灯,规定销售单价不低于成本价,又不高于每台32元.销售中平均每月销售量y(台)与销售单价x(元)的关系可以近似地看做一次函数,如下表所示:
x | 22 | 24 | 26 | 28 |
y | 90 | 80 | 70 | 60 |
(1)请直接写出y与x之间的函数关系式;
(2)为了实现平均每月375元的台灯销售利润,这种台灯的售价应定为多少?这时每月应购进台灯多少个?
(3)设超市每月台灯销售利润为ω(元),求ω与x之间的函数关系式,当x取何值时,ω的值最大?最大值是多少?
【答案】(1)y=﹣5x+200;(2)这种台灯的售价应定25元,这时每月应购进台灯75个;(3)当x=30时,ω取得最大值,最大值是500
【解析】
(1)根据表格中的数据可以求得y与x之间的函数关系式;
(2)根据题意可以得到相应的方程,从而可以解答本题;
(3)根据题意可以求得ω与x之间的函数关系式,当x取何值时,ω的值最大,最大值是多少.
(1)设y与x之间的函数关系式是y=kx+b,
![]() ,得
,得![]() ,
,
即y与x之间的函数关系式是y=-5x+200;
(2)由题意可得,
(x-20)(-5x+200)=375,
解得,x1=25,x2=35(舍去),
y=-5×25+200=75,
答:这种台灯的售价应定25元,这时每月应购进台灯75个;
(3)由题意可得,
ω=(x-20)(-5x+200)=-5(x-30)2+500,
∵20≤x≤32,
∴当x=30时,ω取得最大值,最大值是500.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的顶点M在第二象限,且经过点 A(1,0)和点 B(0,2).则
(1)a 的取值范围是________;
(2)若△AMO的面积为△ABO面积的![]() 倍时,则a的值为________
倍时,则a的值为________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共![]() 个,小李做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,如表是实验中的一组统计数据:
个,小李做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,如表是实验中的一组统计数据:
摸球的次数 |
|
|
|
|
|
|
|
摸到白球的次数 |
|
|
|
|
|
|
|
摸到白球的频率 |
|
|
|
|
|
|
|
![]() 请估计:当实验次数为
请估计:当实验次数为![]() 次时,摸到白球的频率将会接近________;(精确到
次时,摸到白球的频率将会接近________;(精确到![]() )
)
![]() 假如你摸一次,你摸到白球的概率
假如你摸一次,你摸到白球的概率![]() (摸到白球)
(摸到白球)![]() ________;
________;
![]() 如何通过增加或减少这个不透明盒子内球的具体数量,使得在这个盒子里每次摸到白球的概率为
如何通过增加或减少这个不透明盒子内球的具体数量,使得在这个盒子里每次摸到白球的概率为![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
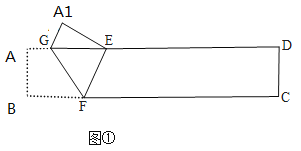
【题目】四边形ABCD是长方形,将长方形ABCD折叠,如图①所示,点B落在AD边上的点E处,折痕为FG,将图②折叠,点C与点E重合,折痕为PH.
(1)在图②中,证明:EH=EP;
(2)若EF=6,EH=8,FH=10,求长方形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象经过点(3,0),对称轴是直线x=﹣2,与y轴的交点(0,﹣3).
(1)求抛物线与x轴的另一个交点坐标;
(2)求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABD,△ACE都是等边三角形,
(1)求证:△ABE≌△ADC;
(2)若∠ACD=15°,求∠AEB的度数;
(3)如图2,当△ABD与△ACE的位置发生变化,使C、E、D三点在一条直线上,求证:AC∥BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个钢筋三角架三边长分别为![]() ,
,![]() ,
,![]() ,现在要做一个和它相似的钢筋三角架,而只有长为
,现在要做一个和它相似的钢筋三角架,而只有长为![]() 和
和![]() 的两根钢筋,要求以其中的一根为一边,从另一根上截两段(允许有余料)作为另两边,则不同的截法有( )
的两根钢筋,要求以其中的一根为一边,从另一根上截两段(允许有余料)作为另两边,则不同的截法有( )
A. 一种 B. 两种 C. 三种 D. 四种或四种以上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)

(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com