
【题目】已知二次函数的图象经过点(3,0),对称轴是直线x=﹣2,与y轴的交点(0,﹣3).
(1)求抛物线与x轴的另一个交点坐标;
(2)求抛物线的解析式.
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是BC边上的中点,G是AC边上一点,过G作EF⊥BC,交BC于点E,交BA的延长线于点F.

(1)求证:AD∥EF;
(2)求证:△AFG是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了丰富学生的课外生活,根据实际情况开设特色活动课,有A:合唱团,B:话剧社,C:舞蹈,D:美术四种项目.为了解学生喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图和扇形统计图.请你结合图中信息解答下列问题:
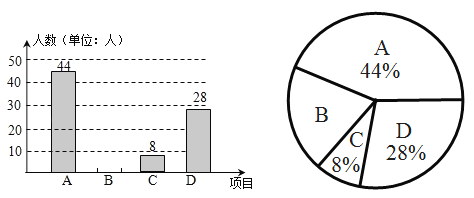
(1)这次调查中总共抽取了_______人,在扇形统计图中,表示B话剧社所对应的圆心角是_______度;
(2)把条形统计图补充完整.
(3)已知该校有2000人,估计全校喜欢话剧的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种成本为每台20元的台灯,规定销售单价不低于成本价,又不高于每台32元.销售中平均每月销售量y(台)与销售单价x(元)的关系可以近似地看做一次函数,如下表所示:
x | 22 | 24 | 26 | 28 |
y | 90 | 80 | 70 | 60 |
(1)请直接写出y与x之间的函数关系式;
(2)为了实现平均每月375元的台灯销售利润,这种台灯的售价应定为多少?这时每月应购进台灯多少个?
(3)设超市每月台灯销售利润为ω(元),求ω与x之间的函数关系式,当x取何值时,ω的值最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,∠B<∠C,AD,AE分别是△ABC的高和角平分线,
(1)若∠B=30°,∠C=50°.则∠DAE的度数是 .(直接写出答案)
(2)写出∠DAE、∠B、∠C的数量关系: ,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数图象的顶点坐标是(3,5),且抛物线经过点A(1,3).
(1)求此抛物线的表达式;
(2)如果点A关于该抛物线对称轴的对称点是B点,且抛物线与y轴的交点是C点,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com