
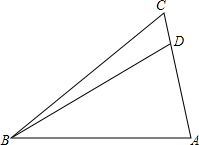
 如图,在△ABC中,已知∠CDB=110°,∠ABD=30°.
如图,在△ABC中,已知∠CDB=110°,∠ABD=30°.分析 (1)首先以A为圆心,小于AC长为半径画弧,交AB、AC两点,再分别以两点为圆心,大于两点之间的距离的一半长为半径画弧,两弧交于一点M,然后作射线AM交BD于E;
(2)利用三角形内角与外角的关系可得∠BAC的度数,再根据角平分线的定义计算出∠EAD的度数,再次利用外角的性质可得答案.
解答 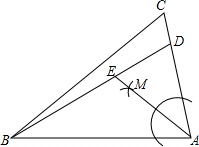 解:(1)如图所示:
解:(1)如图所示:
(2)∵∠CDB=110°,∠ABD=30°.
∴∠CAB=110°-30°=80°,
∵AE平分∠CAB,
∴∠DAE=40°,
∴∠DEA=110°-40°=70°.
点评 此题主要考查了基本作图,以及角的计算,关键是掌握角平分线的作法,以及三角形的外角等于与它不相邻的两个内角的和.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{b±\sqrt{b^2-4ac}}{2a}$ | B. | $\frac{-b+\sqrt{b^2-4ac}}{2a}$ | C. | $\frac{-b±\sqrt{b^2-4ac}}{2}$ | D. | $\frac{-b±\sqrt{b^2-4ac}}{2a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
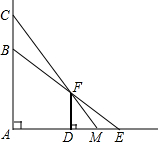 如图,一只猫头鹰蹲在树AC上的B处,通过墙顶F发现一只老鼠在E处,刚想起飞捕捉时,老鼠突然跑到矮墙DF的阴影下,猫头鹰立即从B处向上飞至树上C处时,恰巧可以通过墙顶F看到老鼠躲在M处(A、D、M、E四点在同一条直线上).
如图,一只猫头鹰蹲在树AC上的B处,通过墙顶F发现一只老鼠在E处,刚想起飞捕捉时,老鼠突然跑到矮墙DF的阴影下,猫头鹰立即从B处向上飞至树上C处时,恰巧可以通过墙顶F看到老鼠躲在M处(A、D、M、E四点在同一条直线上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知等边三角形ABC,D为AC上一点,CD=CE,∠ACE=60°,延长BD交AE于F,连接CF.
如图,已知等边三角形ABC,D为AC上一点,CD=CE,∠ACE=60°,延长BD交AE于F,连接CF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com