
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4)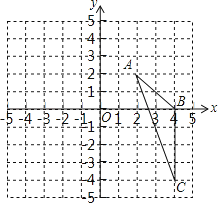
(1)请画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的 ![]() ,得到△A2B2C2 , 请在y轴右侧画出△A2B2C2 , 并求出∠A2C2B2的正弦值.
,得到△A2B2C2 , 请在y轴右侧画出△A2B2C2 , 并求出∠A2C2B2的正弦值.
【答案】
(1)
解:请画出△ABC向左平移6个单位长度后得到的△A1B1C1,如图1所示,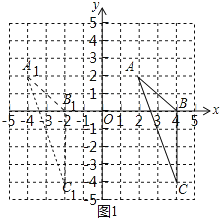
(2)
解:以点O为位似中心,将△ABC缩小为原来的 ![]() ,得到△A2B2C2,请在y轴右侧画出△A2B2C2,如图2所示,
,得到△A2B2C2,请在y轴右侧画出△A2B2C2,如图2所示, 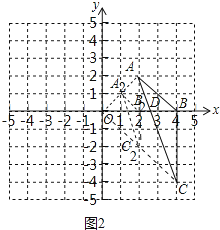
∵A(2,2),C(4,﹣4),B(4,0),
∴直线AC解析式为y=﹣3x+8,与x轴交于点D( ![]() ,0),
,0),
∵∠CBD=90°,
∴CD= ![]() =
= ![]()
![]() ,
,
∴sin∠DCB= ![]() =
= ![]() =
= ![]() .
.
∵∠A2C2B2=∠ACB,
∴sin∠A2C2B2=sin∠DCB= ![]()
【解析】本题考查位似变换、平移变换等知识,锐角三角函数等知识,解题的关键是理解位似变换、平移变换的概念,记住锐角三角函数的定义,属于中考常考题型.


科目:初中数学 来源: 题型:
【题目】已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E. 
(1)求证:ACAD=ABAE;
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荔枝是深圳的特色水果,小明的妈妈先购买了2千克桂味和3千克糯米糍,共花费90元;后又购买了1千克桂味和2千克糯米糍,共花费55元.(每次两种荔枝的售价都不变)
(1)求桂味和糯米糍的售价分别是每千克多少元;
(2)如果还需购买两种荔枝共12千克,要求糯米糍的数量不少于桂味数量的2倍,请设计一种购买方案,使所需总费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C,E是直线l两侧的点,以C为圆心,CE长为半径画弧交l于A,B两点,又分别以A,B为圆心,大于 ![]() AB的长为半径画弧,两弧交于点D,连接CA,CB,CD,下列结论不一定正确的是( )
AB的长为半径画弧,两弧交于点D,连接CA,CB,CD,下列结论不一定正确的是( ) 
A.CD⊥l
B.点A,B关于直线CD对称
C.点C,D关于直线l对称
D.CD平分∠ACB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙二人在环形跑道上同时同地出发,同向运动.若甲的速度是乙的速度的2倍,则甲运动2周,甲、乙第一次相遇;若甲的速度是乙的速度3倍,则甲运动 ![]() 周,甲、乙第一次相遇;若甲的速度是乙的速度4倍,则甲运动
周,甲、乙第一次相遇;若甲的速度是乙的速度4倍,则甲运动 ![]() 周,甲、乙第一次相遇,…,以此探究正常走时的时钟,时针和分针从0点(12点)同时出发,分针旋转周,时针和分针第一次相遇.
周,甲、乙第一次相遇,…,以此探究正常走时的时钟,时针和分针从0点(12点)同时出发,分针旋转周,时针和分针第一次相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,A,E为格点,B,F为小正方形边的中点,C为AE,BF的延长线的交点.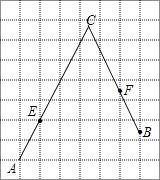
(1)AE的长等于;
(2)若点P在线段AC上,点Q在线段BC上,且满足AP=PQ=QB,请在如图所示的网格中,用无刻度的直尺,画出线段PQ,并简要说明点P,Q的位置是如何找到的(不要求证明) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
x | … | 1 | 2 | 3 | 5 | 7 | 9 | … |
y | … | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | … |
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为
②该函数的一条性质:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一列按一定顺序和规律排列的数:
第一个数是 ![]() ;
;
第二个数是 ![]() ;
;
第三个数是 ![]() ;
;
…
对任何正整数n,第n个数与第(n+1)个数的和等于 ![]() .
.
(1)经过探究,我们发现: ![]()
设这列数的第5个数为a,那么 ![]() ,
, ![]() ,
, ![]() ,哪个正确?
,哪个正确?
请你直接写出正确的结论;
(2)请你观察第1个数、第2个数、第3个数,猜想这列数的第n个数(即用正整数n表示第n数),并且证明你的猜想满足“第n个数与第(n+1)个数的和等于 ![]() ”;
”;
(3)设M表示 ![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() ,这2016个数的和,即
,这2016个数的和,即 ![]() ,
,
求证: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】林业部门要考察某种幼树在一定条件下的移植成活率,下表是这种幼树在移植过程中的一组数据:
移植的棵数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
成活的棵数m | 865 | 1356 | 2220 | 3500 | 7056 | 13170 | 17580 | 26430 |
成活的频率 | 0.865 | 0.904 | 0.888 | 0.875 | 0.882 | 0.878 | 0.879 | 0.881 |
估计该种幼树在此条件下移植成活的概率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com