
【题目】荔枝是深圳的特色水果,小明的妈妈先购买了2千克桂味和3千克糯米糍,共花费90元;后又购买了1千克桂味和2千克糯米糍,共花费55元.(每次两种荔枝的售价都不变)
(1)求桂味和糯米糍的售价分别是每千克多少元;
(2)如果还需购买两种荔枝共12千克,要求糯米糍的数量不少于桂味数量的2倍,请设计一种购买方案,使所需总费用最低.
【答案】
(1)
解:设桂味的售价为每千克x元,糯米糍的售价为每千克y元;
根据题意得: ![]() ,
,
解得: ![]() ;
;
答:桂味的售价为每千克15元,糯米糍的售价为每千克20元.
(2)
解:设购买桂味t千克,总费用为W元,则购买糯米糍(12﹣t)千克,
根据题意得:12﹣t≥2t,
∴t≤4,
∵W=15t+20(12﹣t)=﹣5t+240,
k=﹣5<0,
∴W随t的增大而减小,
∴当t=4时,W的最小值=220(元),此时12﹣4=8;
答:购买桂味4千克,糯米糍8千克时,所需总费用最低.
【解析】(1)设桂味的售价为每千克x元,糯米糍的售价为每千克y元;根据单价和费用关系列出方程组,解方程组即可;
(2)设购买桂味t千克,总费用为W元,则购买糯米糍(12﹣t)千克,根据题意得出12﹣t≥2t,得出t≤4,由题意得出W=﹣5t+240,由一次函数的性质得出W随t的增大而减小,得出当t=4时,W的最小值=220(元),求出12﹣4=8即可. 本题考查了一次函数的应用、二元一次方程组的应用;根据题意方程方程组和得出一次函数解析式是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在如图所示的网格中,线段AB和直线a如图所示,方格纸中每个小正方形的边长均为1,线段AB的两个端点均在格点上.
(1)在图中画出以线段AB为一边的正方形 ABCD,且点C和点D均在格点上,
并直接写出正方形 ABCD的面积为 ;
(2)在图中以线段AB为一腰的等腰三角形ABE,点E在格点上,则满足条件的点E有_____ 个;
(3)在图中的直线a上找一点Q,使得△QAB的周长最小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=3,BC=5,以点B为圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于 ![]() PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为
PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为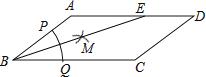
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30o,点A1、A2、A3 在射线ON上,点B1、B2、B3…..在射线OM上,△A1B1A2. △A2B2A3、△A3B3A4……均为等边三角形,若OA1=l,则△A6B6A7 的边长为【 】

A.6 B.12 C.32 D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线a∥b,△ABC是等边三角形,点A在直线a上,边BC在直线b上,把△ABC沿BC方向平移BC的一半得到△A′B′C′(如图①);继续以上的平移得到图②,再继续以上的平移得到图③,…;请问在第2018个图形中等边三角形的个数是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,∠ACB=90°,AC=6cm,BC =8cm.点P从A点出发,沿![]() 路径向终点B运动,点Q从B点出发,沿
路径向终点B运动,点Q从B点出发,沿![]() 路径向终点A运动.点P 和Q分别
路径向终点A运动.点P 和Q分别![]() 和
和![]() 的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过点P和Q作PE⊥l于E,QF⊥l于F.则点P运动多少秒时,△PEC和△CFQ全等?请说明理由.
的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过点P和Q作PE⊥l于E,QF⊥l于F.则点P运动多少秒时,△PEC和△CFQ全等?请说明理由.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com