
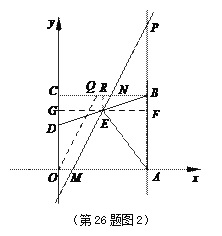
【题目】(本题12分)如图,O是坐标原点,矩形OABC的顶点A在x轴的正半轴上,点C在y轴的正半轴上,点D在边OC上,点B(6,5),且![]() .
.
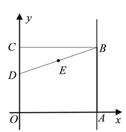
(1)填空:CD的长为_____________;
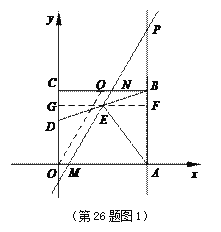
(2)若点E是BD的中点,将过点E的直线l绕着点E旋转,分别与直线OA、BC相交于点M、N,与直线AB相交于点P,连结AE.
①设点P的纵坐标为t,当△PBE∽△PEA时,求t的值;
②试问:在旋转的过程中,线段MN与BD能否相等?若能,请求出CN的长;若不能,请说明理
【答案】【答案】(1) ![]() (2)
(2) ![]() (3)
(3)![]() 与
与![]() 能相等,理由见解析.
能相等,理由见解析.
【解析】(1)根据点B的坐标,可得BC=6.利用tan∠CBD=![]() ,即可解答;
,即可解答;
(2)①当△PBE∽△PEA时, ![]() =
=![]() ,即PE2=PA×PB. 过E作FG∥BC分别交OC、AB于G、F,得到GE是三角形BCD的中位线,从而得到BF=CG=
,即PE2=PA×PB. 过E作FG∥BC分别交OC、AB于G、F,得到GE是三角形BCD的中位线,从而得到BF=CG=![]() CD=1,GE=
CD=1,GE=![]() BC=3,AF=4,EF=3,由PA=t,PB=t-5,PE=t-4,利用勾股定理得,PE2=PF2+EF2=(t-4)2+32,根据PE2= PA×PB=|t(t-5)|,得到(t-4)2+32=t(t-5),解方程即可解答;
BC=3,AF=4,EF=3,由PA=t,PB=t-5,PE=t-4,利用勾股定理得,PE2=PF2+EF2=(t-4)2+32,根据PE2= PA×PB=|t(t-5)|,得到(t-4)2+32=t(t-5),解方程即可解答;
②MN与BD能相等,理由如下:利用在矩形OABC中,∠BCO=90°,CD=2,BC=6,求出BD=![]() =2
=2![]() ,如图2,过O作OQ∥MN,交BC于点Q,则OQ=MN=BD=2
,如图2,过O作OQ∥MN,交BC于点Q,则OQ=MN=BD=2![]() ,CQ=
,CQ=![]() ,从而确定(
,从而确定(![]() ,5),求出直线OQ的函数关系式为y=
,5),求出直线OQ的函数关系式为y=![]() x,直线MN的函数关系式为y=
x,直线MN的函数关系式为y=![]() x+4-
x+4-![]() ,令y=5,得
,令y=5,得![]() x+4-
x+4-![]() =5,
=5,
解得:x=![]() ,所以N1(
,所以N1( ![]() ,5)由矩形对称性得:N2(
,5)由矩形对称性得:N2(![]() ,5)所以CN=
,5)所以CN=![]() 也符合题意.
也符合题意.
解:(1) ![]() ;
;
(2) ①方法一:当![]() ∽
∽![]() 时,
时, ![]() ,即
,即![]() .
.
过![]() 作
作![]() 分别交
分别交![]() 、
、![]() 于
于![]() 、
、![]() ,则
,则![]() 是
是![]() 的中位线,
的中位线,
∴![]() ,
,
∴![]() ,
, ![]() ,
,
∵![]() ,
, ![]() ,
, ![]() ,
,
由勾股定理得, ![]() ,
,
∴![]() .
.
由![]() 解得
解得![]() ,
,
由![]() 得,
得, ![]() ,此方程没有实数根,
,此方程没有实数根,
∴![]() ;
;
方法二:求出![]() ,
, ![]() ,
,
当![]() ∽
∽![]() 时,
时, ![]() ,即
,即![]() ,
,
∴![]() ,整理得,
,整理得, ![]() .
.
解得![]() ,
, ![]() (不合题意舍去).∴
(不合题意舍去).∴![]() ;
;
②方法一: ![]() 与
与![]() 能相等,理由如下:
能相等,理由如下:
在矩形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,
,
过![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() ,
, ![]() ,
,
∴![]() ,直线
,直线![]() 的函数关系式为
的函数关系式为![]() .
.
设直线![]() 的函数关系式为
的函数关系式为![]() ,把
,把![]() 代入得,
代入得, ![]() ,
,
解得![]() ,即直线
,即直线![]() 的函数关系式为
的函数关系式为![]() .
.
令![]() ,得
,得![]() ,解得
,解得![]() ,
,
∴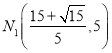 .由矩形的对称性得,
.由矩形的对称性得, 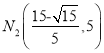 .∴
.∴![]() 也符合题意.
也符合题意.
故![]() .
.
方法二: ![]() 与
与![]() 能相等,理由如下:
能相等,理由如下:
在矩形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() .
.
若![]() ,如图,过
,如图,过![]() 作
作![]() ,
,
交![]() 于点
于点![]() ,过
,过![]() 作
作![]() ⊥
⊥![]() 于
于![]() .
.
则![]() ,
, ![]() ,△
,△![]() ∽△
∽△![]() ,
,
又![]() ,
, ![]() ,
,
∴![]() ,即
,即![]() . ∴
. ∴![]() .
.
根据矩形的对称性, ![]() .
.
∴![]() .
.
“点睛”本题属于几何变换综合题,考查了相似三角形的性质和判定、勾股定理、旋转的性质、待定系数法求解析式,解决本题的关键是辅助线的作法,结合图象用待定系数法求直线的解析式.


科目:初中数学 来源: 题型:
【题目】下列四组线段能构成直角三角形的是( )
A. a=1,b=2,c=3 B. a=2,b=3,c=4
C. a=2,b=4,c=5 D. a=3,b=4,c=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线________.
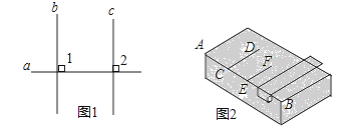
(1)它的理由如下:(如图1)
∵b⊥a,c⊥a,∴∠1=∠2=90°,
∴b∥c________
(2)如图2是木工师傅使用角尺画平行线,有什么道理?________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
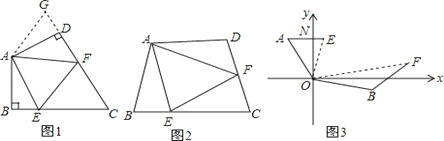
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=![]() ∠BAD上述结论是否仍然成立,并说明理由;
∠BAD上述结论是否仍然成立,并说明理由;
(3)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图形填空:
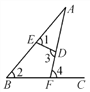
(1)若直线ED,BC被直线AB所截,则∠1和__________是同位角.
(2)若直线ED,BC被直线AF所截,则∠3和__________是内错角.
(3)∠1和∠3是直线AB,AF被直线__________所截构成的__________角.
(4)∠2和∠4是直线__________,__________被直线BC所截构成的__________角.
查看答案和解析>>
科目:初中数学 来源: 题型:
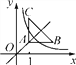
【题目】如图,等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB,AC分别平行于x轴、y轴,若双曲线y=![]() (k≠0)与△ABC有交点,则k的取值范围是____.
(k≠0)与△ABC有交点,则k的取值范围是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
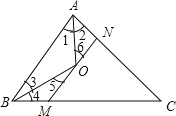
【题目】如图,已知△ABC中,AC+BC=24,AO,BO分别是角平分线,且MN∥BA,分别交AC于N,BC于M,则△CMN的周长为( )
A.12 B.24 C.36 D.不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列结论中正确的是( )
A.三角形的三个内角中最多有一个锐角
B.三角形的三条高都在三角形内
C.钝角三角形最多有一个锐角
D.三角形的三条角平分线都在三角形内部
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com