
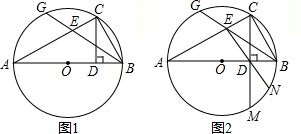
分析 (1)如图1,延长CD交⊙O于点F,由垂径定理可知,2CD=CF,所以只需要证明BG=CF即可;
(2)由勾股定理可求得AC=10,再利用$\widehat{BF}$=$\widehat{BC}$,可知∠CBG=∠BAC,所以可证明△BCE∽△ACB,然后利用对应边的比相等即可求出CE;
(3)过点E作EI⊥AB于点I,过点N作NH⊥AB于点H,作NF⊥CM于点F,连接ON,利用相似三角形的性质和勾股定理分别求出BD、EI、ID的长度,并求出$\frac{NH}{DH}$的比值,利用勾股定理求出NH、DH的长度,进而求出MN的长度.
解答 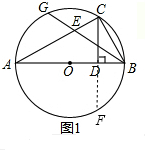 (1)证明:如图1,延长CD交⊙O于点F,
(1)证明:如图1,延长CD交⊙O于点F,
∵CD⊥AB,
∴$\widehat{BF}$=$\widehat{BC}$,CF=2CD,
∵$\widehat{CG}$=$\widehat{CB}$,
∴$\widehat{BF}$=$\widehat{BC}$=$\widehat{CG}$,
∴$\widehat{FC}$=$\widehat{BG}$,
∴BG=CF,
∵CF=2CD
∴BG=2CD;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=5$\sqrt{5}$,BC=5,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=10,
∵$\widehat{CG}$=$\widehat{CB}$,
∴∠CBG=∠BAC,
∵∠BCE=∠ACB,
∴△BCE∽△ACB,
∴$\frac{EC}{BC}=\frac{BC}{AC}$,
∴$\frac{CE}{5}=\frac{5}{10}$,
∴CE=2.5;
(3)过点E作EI⊥AB于点I,过点N作NH⊥AB于点H,作NF⊥CM于点F,
连接ON,
易证△BCD∽△CAB,
∴BC2=BD•AB,
∴BD=$\sqrt{5}$,
∴AD=5$\sqrt{5}$-$\sqrt{5}$=4$\sqrt{5}$,
由(2)可知:CE=$\frac{5}{2}$,
∴AE=10-$\frac{5}{2}$=$\frac{15}{2}$,
∵EI∥CD,
∴△AEI∽△ACD,
∴$\frac{AE}{AC}=\frac{AI}{AD}$,
∴AI=3$\sqrt{5}$,
∴DI=AD-AI=$\sqrt{5}$,
由勾股定理可求得:EI=$\frac{3\sqrt{5}}{2}$
∵EI∥HN,
∴△EID∽△NHD,
∴$\frac{EI}{ID}=\frac{NH}{DH}$,
∴$\frac{NH}{DH}$=$\frac{3}{2}$,
设NH=3x,DH=2x,
∵OD=OB-BD=$\frac{3}{2}$$\sqrt{5}$,
∴OH=OD+DH=$\frac{3}{2}\sqrt{5}$+2x,
在Rt△OHN中,
由勾股定理可得:($\frac{5}{2}$$\sqrt{5}$)2=($\frac{3}{2}\sqrt{5}$+2x)2+(3x)2,
∴13x2+6$\sqrt{5}$x-20=0,
x=$\frac{-3\sqrt{5}±\sqrt{305}}{13}$,
∵x>0,
∴x=$\frac{-3\sqrt{5}+\sqrt{305}}{13}$
由勾股定理可知:CD=2$\sqrt{5}$,
∴DM=CD=2$\sqrt{5}$,
∴MF=2$\sqrt{5}$-3x,NF=DH=2x,
∴由勾股定理可求得:MN2=MF2+DH2,
∴MN2=20-12$\sqrt{5}$x+13x2=40-18$\sqrt{5}$x=$\frac{790-90\sqrt{61}}{13}$,
∴MN=$\sqrt{\frac{790-90\sqrt{61}}{13}}$
点评 本题考查了圆周角定理、圆心角定理、勾股定理以及相似三角形的判定和性质,用到的知识点很多,对学生综合运用知识的能力要求很高.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1,1) | B. | (-$\frac{1}{2}$,-$\frac{1}{2}$) | C. | (0,-1) | D. | ($\frac{1}{2},-\frac{1}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
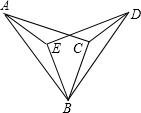 如图,在△ABC和△BDE中,∠ACB=∠DEB=90°,AC=DE,AB=BD,则下列说法不正确的是( )
如图,在△ABC和△BDE中,∠ACB=∠DEB=90°,AC=DE,AB=BD,则下列说法不正确的是( )| A. | BC=BE | B. | ∠BAC=∠BDE | C. | AE=CD | D. | ∠BAC=∠ABC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
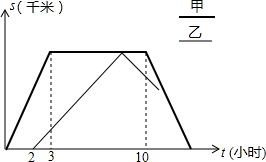 甲乙两 车从A市去往B市,甲比乙早出发了2个小时,甲到达B市后停留一段时间返回,乙到达B市后立即返回.甲车往返的速度都为40千米/时,乙车往返的速度都为20千米/时,如图是两车距A市的路程S(千米)与行驶时间t(小时)之间的函数图象,请结合图象回答下列问题:
甲乙两 车从A市去往B市,甲比乙早出发了2个小时,甲到达B市后停留一段时间返回,乙到达B市后立即返回.甲车往返的速度都为40千米/时,乙车往返的速度都为20千米/时,如图是两车距A市的路程S(千米)与行驶时间t(小时)之间的函数图象,请结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com