
 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:填空题
 复习课上,张老师念了这样一道题目:已知二次函数y=ax2+bx+c的图象如图所示,“三位同学”分别说出了它的一些结论.“可心”说:①a+b+c<0;②a-b+c>1;“童谣”说:③abc>0;④4a-2b+c<0;“思宇”说:⑤c-a>1.请你根据图找出其中正确结论的序号是①②③⑤.
复习课上,张老师念了这样一道题目:已知二次函数y=ax2+bx+c的图象如图所示,“三位同学”分别说出了它的一些结论.“可心”说:①a+b+c<0;②a-b+c>1;“童谣”说:③abc>0;④4a-2b+c<0;“思宇”说:⑤c-a>1.请你根据图找出其中正确结论的序号是①②③⑤.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
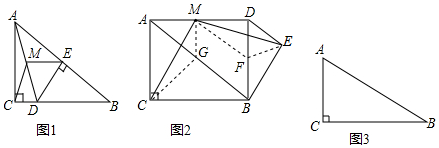
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=-1 | B. | x=-4 | C. | x=-2 | D. | x=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点P、Q是∠AOB内部的两个定点,点M是∠AOB内部的一点,且点M到OA、OB的距离相等,点M到点P、点Q的距离相等,请利用直尺和圆规作出点M.(不写作法,保留作图痕迹)
如图,点P、Q是∠AOB内部的两个定点,点M是∠AOB内部的一点,且点M到OA、OB的距离相等,点M到点P、点Q的距离相等,请利用直尺和圆规作出点M.(不写作法,保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
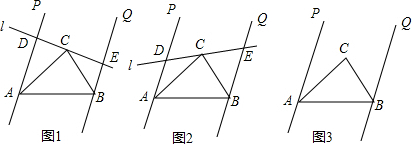
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读下列材料:小华遇到这样一个问题:
阅读下列材料:小华遇到这样一个问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com