
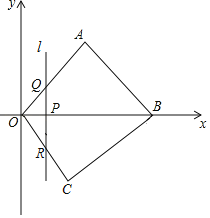
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЫФБпаЮOABCЕФЖЅЕуOЪЧзјБъдЕуЃЌЁЯOABЃН90ЁуЧвOAЃНABЃЌOBЃН8ЃЌOCЃН5ЃЎ
ЃЈ1ЃЉЧѓЕуAЕФзјБъЃЛ
ЃЈ2ЃЉЕуPЪЧДгOЕуГіЗЂЃЌбиXжсе§АыжсЗНЯђвдУПУы1ЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏжСЕуBЕФвЛИіЖЏЕуЃЈЕуPВЛгыЕуOЃЌBжиКЯЃЉЃЌЙ§ЕуPЕФжБЯпlгыyжсЦНааЃЌНЛЫФБпаЮABCDЕФБпAOЛђABгкЕуQЃЌНЛOCЛђBCгкЕуRЃЎЩшдЫЖЏЪБМфЮЊtЃЈsЃЉЃЌвбжЊtЃН3ЪБЃЌжБЯпlЧЁКУОЙ§Еу CЃЎ
ЧѓЂйЕуPГіЗЂЪБЭЌЪБЕуEвВДгЕуBГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШЯђЕуOдЫЖЏЃЌЕуPЭЃжЙЪБЕуEвВЭЃжЙЃЎЩшЁїQREЕФУцЛ§ЮЊSЃЌЧѓЕБ0ЃМtЃМ3ЪБSгыtЕФКЏЪ§ЙиЯЕЪНЃЛВЂжБНгаДГіSЕФзюДѓжЕЃЎ
ЂкЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙЕУЁїOREЮЊжБНЧШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіЯргІtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉAЃЈ4ЃЌ4ЃЉЃЛЃЈ2ЃЉЂй![]() ЃЌSгазюДѓжЕЮЊ
ЃЌSгазюДѓжЕЮЊ![]() ЃЛЂкtЕФжЕЮЊ4Лђ
ЃЛЂкtЕФжЕЮЊ4Лђ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉЂйЪзЯШЧѓГіжБЯпOAЁЂOBЁЂOCЁЂBCЕФНтЮіЪНЃЎЂйЧѓГіPЁЂQЕФзјБъМДПЩНтОіЮЪЬтЃЛМДПЩБэЪОГіQRКЭPEЕФГЄЃЌМДПЩЕУЕНШ§НЧаЮУцЛ§НтЮіЪНРћгУХфЗНЗЈЧѓГізюжЕМДПЩЃЛ
ЂкЗжШ§жжЧщПіЬжТлЃЌМДЁЯREOЃН90ЁуЛђЁЯOREЃН90ЁуЛђЁЯROEЃН90ЁуЗжБ№ЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉгЩЬтвтЁїOABЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁпOBЃН8ЃЌМДBЃЈ8ЃЌ0ЃЉ
ЁрAЃЈ4ЃЌ4ЃЉЃЌ
ЃЈ2ЃЉЁпAЃЈ4ЃЌ4ЃЉЃЌBЃЈ8ЃЌ0ЃЉЃЌ
ЁржБЯпOAЕФНтЮіЪНЮЊyЃНxЃЌжБЯпABЕФНтЮіЪНyЃНЉx+6ЃЌ
ЁпtЃН3ЪБЃЌжБЯпlЧЁКУЙ§ЕуCЃЌМДOPЃН3ЃЌOCЃН5ЃЌ
ЁрPRЃН4ЃЌCЃЈ3ЃЌЉ4ЃЉЃЌ
ЁржБЯпOCЕФНтЮіЪНЮЊyЃН-![]() xЃЌжБЯпBCЕФНтЮіЪНЮЊyЃН
xЃЌжБЯпBCЕФНтЮіЪНЮЊyЃН![]() ЃЌ
ЃЌ
ЂйЕБ0ЃМtЃМ3ЪБЃЌQЃЈtЃЌtЃЉЃЌRЃЈtЃЌ-![]() tЃЉЃЌ
tЃЉЃЌ
ЁрQR=t-(-![]() t)=
t)=![]() ЃЎPEЃН8Љ2tЃЎ
ЃЎPEЃН8Љ2tЃЎ
ЁрSЃН![]() ЃЎ
ЃЎ
ЁрtЃН2ЪБЃЌSгазюДѓжЕЮЊ![]() ЃЎ
ЃЎ
ЂквЊЪЙЁїOREЮЊжБНЧШ§НЧаЮЃЌдђгаШ§жжЧщПіЃК
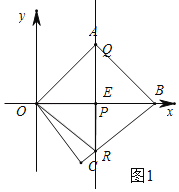
ЂёЃЎШєЁЯREOЃН90ЁуЃЌШчЭМ1ЃЌдђЕуPгыEЕужиКЯЃЌ
Ёр8Љ2tЃН0ЃЌНтЕУtЃН4ЃЌ
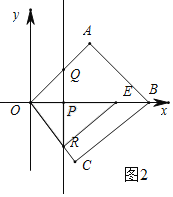
ЂђЃЎШєЁЯOREЃН90ЁуЃЌШчЭМ2ЃЎЁїORPЁзЁїREPЃЌ
Ёр![]() ЃЌМДRP2ЃНOPPEЃЌ
ЃЌМДRP2ЃНOPPEЃЌ
Ёр![]() ЃЌ
ЃЌ
НтжЎЕУЃКtЃН![]() ЃЌ
ЃЌ
Ђѓ
ЙЪЪЙЕУЁїOREЮЊжБНЧШ§НЧаЮЪБЃЌtЕФжЕЮЊЃК4Лђ![]() ЃЌ
ЃЌ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкОиаЮABCDжаЃЌABЃН6ЃЌADЃН8ЃЌЕуEЪЧБпADЩЯвЛЕуЃЌEMЁЭBCНЛABгкЕуMЃЌЕуNдкЩфЯпMBЩЯЃЌЧвAEЪЧAMКЭANЕФБШР§жаЯюЃЎ
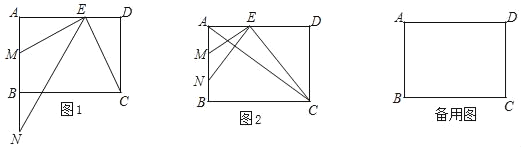
ЃЈ1ЃЉШчЭМ1ЃЌЧѓжЄЃКЁЯANEЃНЁЯDCEЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуNдкЯпЖЮMBжЎМфЃЌСЊНсACЃЌЧвACгыNEЛЅЯрДЙжБЃЌЧѓMNЕФГЄЃЛ
ЃЈ3ЃЉСЌНгACЃЌШчЙћЁїAECгывдЕуEЁЂMЁЂNЮЊЖЅЕуЫљзщГЩЕФШ§НЧаЮЯрЫЦЃЌЧѓDEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇЯАаЁзщгЩ3УћФаЩњКЭ1УћХЎЩњзщГЩЃЌдквЛДЮКЯзїбЇЯАКѓЃЌПЊЪМНјааГЩЙћеЙЪОЃЎ
ЃЈ1ЃЉШчЙћЫцЛњГщШЁ1УћЭЌбЇЕЅЖРеЙЪОЃЌФЧУДХЎЩњеЙЪОЕФИХТЪЮЊ ЃЛ
ЃЈ2ЃЉШчЙћЫцЛњГщШЁ2УћЭЌбЇЙВЭЌеЙЪОЃЌЧѓЭЌЮЊФаЩњЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌRtЁїABCжаЃЌЁЯC=90ЁуЃЌЁЯABC=30ЁуЃЌAC=2ЃЌЁїABCШЦЕуCЫГЪБеыа§зЊЕУЁїA1B1CЃЌЕБA1ТфдкABБпЩЯЪБЃЌСЌНгB1BЃЌШЁBB1ЕФжаЕуDЃЌСЌНгA1DЃЌдђA1DЕФГЄЖШЪЧ ЃЈЁЁЁЁЃЉ

A. ![]() B. 2
B. 2![]() C. 3 D. 2
C. 3 D. 2![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯп![]() гы
гы![]() жсЃЌ
жсЃЌ ![]() жсЗжБ№НЛгкЕуAЁЂBЃЌХзЮяЯп
жсЗжБ№НЛгкЕуAЁЂBЃЌХзЮяЯп![]() ОЙ§ЕуAКЭЕуBЃЌгыxжсЕФСэвЛИіНЛЕуЮЊCЃЌЖЏЕуDДгЕуAГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђOЕудЫЖЏЃЌЭЌЪБЖЏЕуEДгЕуBГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЯђAЕудЫЖЏЃЌЩшдЫЖЏЕФЪБМфЮЊtУыЃЌ0ЉtЉ5.
ОЙ§ЕуAКЭЕуBЃЌгыxжсЕФСэвЛИіНЛЕуЮЊCЃЌЖЏЕуDДгЕуAГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђOЕудЫЖЏЃЌЭЌЪБЖЏЕуEДгЕуBГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШЯђAЕудЫЖЏЃЌЩшдЫЖЏЕФЪБМфЮЊtУыЃЌ0ЉtЉ5.
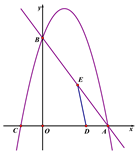
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБtЮЊКЮжЕЪБЃЌвдAЁЂDЁЂEЮЊЖЅЕуЕФШ§НЧаЮгыЁїAOBЯрЫЦЃЛ
ЃЈ3ЃЉЕБЁїADEЮЊЕШбќШ§НЧаЮЪБЃЌЧѓtЕФжЕЃЛ
ЃЈ4ЃЉХзЮяЯпЩЯЪЧЗёДцдквЛЕуFЃЌЪЙЕУвдAЁЂBЁЂDЁЂFЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌжБНгаДГіFЕуЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌABЃН4ЃЌADЃН6ЃЌЕуEЮЊADЕФжаЕуЃЌЕуPЮЊЯпЖЮABЩЯвЛИіЖЏЕуЃЌСЌНгEPЃЌНЋЁїAPEбиEPелЕўЕУЕНЁїEPFЃЌСЌНгCEЃЌCFЃЌЕБЁїECFЮЊжБНЧШ§НЧаЮЪБЃЌAPЕФГЄЮЊ______.
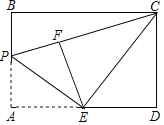
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
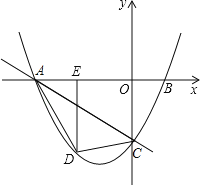
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃН-![]() x-3гыxжсЃЌyжсЗжБ№НЛгкЕуAЃЌCЃЌОЙ§ЕуAЃЌCЕФХзЮяЯпyЃНax2+bxЉ3гыxжсЕФСэвЛИіНЛЕуЮЊЕуB(2ЃЌ0)ЃЌЕуDЪЧХзЮяЯпЩЯвЛЕуЃЌЙ§ЕуDзїDEЁЭxжсгкЕуEЃЌСЌНгADЃЌDCЃЎЩшЕуDЕФКсзјБъЮЊmЃЎ
x-3гыxжсЃЌyжсЗжБ№НЛгкЕуAЃЌCЃЌОЙ§ЕуAЃЌCЕФХзЮяЯпyЃНax2+bxЉ3гыxжсЕФСэвЛИіНЛЕуЮЊЕуB(2ЃЌ0)ЃЌЕуDЪЧХзЮяЯпЩЯвЛЕуЃЌЙ§ЕуDзїDEЁЭxжсгкЕуEЃЌСЌНгADЃЌDCЃЎЩшЕуDЕФКсзјБъЮЊmЃЎ
(1)ЧѓХзЮяЯпЕФНтЮіЪНЃЛ
(2)ЕБЕуDдкЕкШ§ЯѓЯоЃЌЩшЁїDACЕФУцЛ§ЮЊSЃЌЧѓSгыmЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГіSЕФзюДѓжЕМАДЫЪБЕуDЕФзјБъЃЛ
(3)СЌНгBCЃЌШєЁЯEADЃНЁЯOBCЃЌЧыжБНгаДГіДЫЪБЕуDЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМКжЊХзЮяЯпy=ax2+bxЃ3a(a>0)гыxжсНЛгкA(Ѓ1,0)ЁЂBСНЕуЃЌгыyжсНЛгкЕуC.
(1)ЧѓЕуBЕФзјБъЃЛ
(2)PЪЧЕкЫФЯѓЯоФкХзЮяЯпЩЯЕФвЛИіЖЏЕу.
ЂйШєЁЯAPB=90ЁуЃЌЧвa<3ЃЌЧѓЕуPзнзјБъЕФШЁжЕЗЖЮЇЃЛ
ЂкжБЯпPAЁЂPBЗжБ№НЛyжсгкЕуMЁЂNЧѓжЄЃК![]() ЮЊЖЈжЕ.
ЮЊЖЈжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁЖОХеТЫуЪѕЁЗЪЧЮвЙњЙХДњЪ§бЇЕФОЕфжјзїЃЌЪщжагавЛИіЮЪЬтЃКЁАНёгаЛЦН№ОХУЖЃЌАзвјвЛЪЎвЛУЖЃЌГЦжЎжиЪЪЕШЃЌНЛвзЦфвЛЃЌН№ЧсЪЎШ§СНЃЌЮЪН№ЁЂвјвЛУЖИїжиМИКЮЃПЁБвтЫМЪЧЃКМзДќжазАгаЛЦН№9УЖЃЈУПУЖЛЦН№жиСПЯрЭЌЃЉЃЌввДќжазАгаАзвј11УЖЃЈУПУЖАзвјжиСПЯрЭЌЃЉЃЌГЦжиСНДќЯрЭЌЃЌСНДќЛЅЯрНЛЛЛ1УЖКѓЃЌМзДќБШввДќЧсСЫ13СНЃЈДќзгжиСПКіТдВЛМЦЃЉЃЌЮЪЛЦН№ЁЂАзвјУПУЖИїжжЖрЩйСНЃПЩшЛЦН№жи![]() СНЃЌУПУЖАзвјжи
СНЃЌУПУЖАзвјжи![]() СНЃЌИљОнЬтвтПЩСаЗНГЬзщЮЊ____.
СНЃЌИљОнЬтвтПЩСаЗНГЬзщЮЊ____.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com