
【题目】已知抛物线C:y=(-a2+a)x2+x+1(a≠0)
(1)无论a为何值,抛物线C总是经过一个定点,该定点的坐标为_____.
(2)无论a为何值,该抛物线的顶点总在一条固定的直线上运动,求出该直线的解析式.
(3)当0<y≤2时,y>0恒成立,求a的取值范围.
【答案】(1)(0,1);(2)![]() ;(3)0<a<1,
;(3)0<a<1,![]() 或
或![]() .
.
【解析】
(1)函数的常数项为1,所以过定点(0,1);
(2)求出顶点坐标公式,令![]() ,代入即可;
,代入即可;
(3))①当-a2+a>0时,即0<a<1,当0<a<1,0<x≤2时,y>0恒成立,②当-a2+a<0时,即a>1或a<0,当0<x≤2时,y>0恒成立则x=2时,y>0;
(1)无论a为何值,抛物线C总是经过一个定点,(0,1);
(2)y=(-a2+a)x2+x+1的顶点为(![]() ,
,![]() ),
),
设x=![]() ,y=
,y=![]() ,
,
则![]() ,
,
∴y=![]() =
=![]() =
=![]() ,
,
(3)①当-a2+a>0时,即0<a<1,
∴抛物线开口向上,对称轴x=![]() 在y轴左侧,
在y轴左侧,
∴当0<x≤2时,y随x的增大而增大,
∴当x=2时,y>0
∴当0<a<1,0<x≤2时,y>0恒成立,
②当-a2+a<0时,即a>1或a<0,
∴抛物线开口向下
∵抛物线与y轴交于点(0,1),
当0<x≤2时,y>0恒成立
∴当x=2时,y>0,
即4(-a2+a)+3>0,
解得![]() 或
或![]() ,
,
综上,0<a<1,![]() 或
或![]() ;
;


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
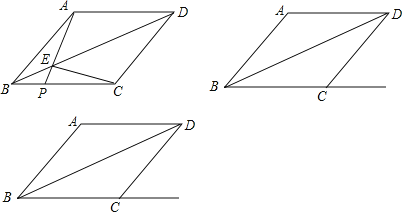
【题目】如图,菱形ABCD中,AB=10,连接BD,点P是射线BC上一点(不与点B重合),AP与对角线BD交于点E,连接EC.
(1)求证:AE=CE;
(2)若sin∠ABD=![]() ,当点P在线段BC上时,若BP=4,求△PEC的面积;
,当点P在线段BC上时,若BP=4,求△PEC的面积;
(3)若∠ABC=45°,当点P在线段BC的延长线上时,请直接写出△PEC是等腰三角形时BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于线段![]() 和点
和点![]() ,当
,当![]() ,且
,且![]() 时,称点
时,称点![]() 为线段
为线段![]() 的“等距点”.特别地,当
的“等距点”.特别地,当![]() ,且
,且![]() 时,称点
时,称点![]() 为线段
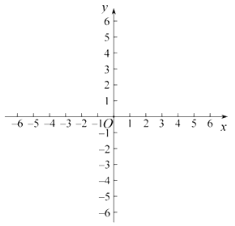
为线段![]() 的“强等距点”.在平面直角坐标系
的“强等距点”.在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() .
.
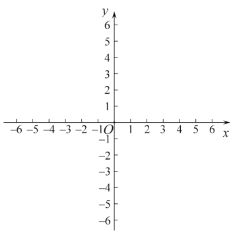
(1)有4个点:![]() ,
,![]() ,
,![]() ,
,![]() .线段
.线段![]() 的“等距点”是 ;其中线段
的“等距点”是 ;其中线段![]() 的“强等距点”是 .
的“强等距点”是 .
(2)设第四象限有一点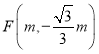 ,点
,点![]() 是线段
是线段![]() 的“强等距点”.
的“强等距点”.
①当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
②当点![]() 又为线段
又为线段![]() 的“等距点”时,求
的“等距点”时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上,点
边上,点![]() 在
在![]() 边上,
边上,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
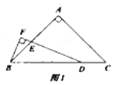
(1)如图1,当![]() 时:①
时:①![]() 的度数为__________;②求证;
的度数为__________;②求证;![]() ;
;
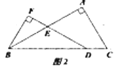
(2)如图2,当![]() 时,求
时,求![]() 的值(用含
的值(用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,对于直线![]() 同侧的
同侧的![]() 、
、![]() 两点,若在
两点,若在![]() 上的点
上的点![]() 满足
满足![]() ,则称
,则称![]() 为
为![]() 、
、![]() 两点在
两点在![]() 上的反射点,
上的反射点,![]() 与
与![]() 的和称为
的和称为![]() 、
、![]() 两点的反射距离.
两点的反射距离.

(1)如图2,在边长为2的正方形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 、
、![]() 两点在直线
两点在直线![]() 上的反射点,求
上的反射点,求![]() 、
、![]() 两点的反射距离;
两点的反射距离;
(2)如图3,![]() 内接于
内接于![]() ,直径
,直径![]() 为4,
为4,![]() ,点
,点![]() 为劣弧
为劣弧![]() 上一动点,点
上一动点,点![]() 为
为![]() 、
、![]() 两点在
两点在![]() 上的反射点,当
上的反射点,当![]() 、
、![]() 两点的反射距离最大时,求劣弧
两点的反射距离最大时,求劣弧![]() 的长;
的长;
(3)如图4,在平面直角坐标系中,抛物线![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,顶点为
,顶点为![]() ,若点
,若点![]() 为点
为点![]() 、
、![]() 在
在![]() 上的反射点,同时点
上的反射点,同时点![]() 为点
为点![]() 、
、![]() 在
在![]() 上的反射点.
上的反射点.
①请判断线段![]() 和
和![]() 的位置关系,并给出证明;
的位置关系,并给出证明;
②求![]() 、
、![]() 两点的反射距离与
两点的反射距离与![]() 、
、![]() 两点的反射距离的比值.
两点的反射距离的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
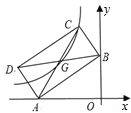
【题目】如图,矩形ABCD的两个顶点A、B分别在x、y轴上,顶点C、D位于第二象限,且OA=3,OB=2,对角线AC、BD交于点G,若双曲线![]() 经过C、G,则k=__________.
经过C、G,则k=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
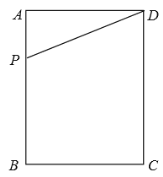
【题目】如图,在矩形ABCD中,AB=4,BC=3,点P是边AB上的一动点,连接DP,
(1)若将△DAP沿DP折叠,点A落在矩形的对角线上点A处,试求AP的长;
(2)点P运动到某一时刻,过点P作直线PE交BC于点E,将△DAP与△PBE分别沿DP与PE折叠,点A与点B分别落在点A,B处,若P,A,B三点恰好在同一直线上,且AB=2,试求此时AP的长.
(3)当点P运动到边AB的中点处时,过点P作直线PG交BC于点G,将△DAP与△PBG分别沿DP与PG折叠,点A与点B重合于点F处,请直接写出F到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
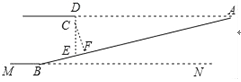
【题目】为缓解交通压力,市郊某地正在修建地铁站,拟同步修建地下停车库.如图是停车库坡道入口的设计图,其中MN是水平线,MN∥AD,AD⊥DE,CF⊥AB,垂足分别为D,F,坡道AB的坡度=1:3,AD=9米,点C在DE上,CD=0.5米,CD是限高标志牌的高度(标志牌上写有:限高 米).如果进入该车库车辆的高度不能超过线段CF的长,则该停车库限高多少米?(结果精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈3.16)
≈3.16)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com