
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() 、
、![]() 分别平分
分别平分![]() 、
、![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.

【答案】(1)见解析;(2)12.
【解析】
(1)延长AE,BC交于M,根据AE、BE分别平分∠BAD、∠ABC,可得出∠AEB=90°,利用ASA证明△ABE≌△MBE,得出AE=ME后,再证明△ADE≌△MCE,即可得出结论.
(2)根据S四边形ABCD=S△ABM=2S△ABE,即可得出答案.
(1)如图,延长AE,BC交于M,
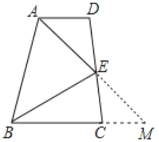
∵AD∥BC,
∴∠DAB+∠ABC=180,
又∵AE、BE分别平分∠BAD、∠ABC,
∴∠DAE=∠EAB,∠ABE=∠MBE,
∴∠EAB+∠ABE=![]() =90,
=90,
∴∠BEA=∠BEM=90゜,
在△ABE和△MBE中,
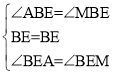
∴△ABE≌△MBE(ASA),
∴AE=ME,
∵AD∥BC
∴∠D=∠ECM
在△ADE和△MCE中,

∴△ADE≌△MCE(AAS),
∴CE=DE.
(2)S△ABE=![]() AE·BE=6,
AE·BE=6,
∵△ADE≌△MCE,AE=ME,
∴S四边形ABCD=S△ABM=2S△ABE=12.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:像(![]() +
+![]() )(
)(![]()
![]() )=3,
)=3,![]()
![]() =a(a≥0),(
=a(a≥0),(![]() +1)(
+1)(![]() ﹣1)=b﹣1(b≥0),……,这种两个含二次根式的代数式相乘,积不含二次根式,我们称这两个代数式互为有理化因式例如:
﹣1)=b﹣1(b≥0),……,这种两个含二次根式的代数式相乘,积不含二次根式,我们称这两个代数式互为有理化因式例如:![]() 与
与![]() ,
,![]() +1与
+1与![]() ﹣1,2
﹣1,2![]() +3
+3![]() 与2
与2![]() ﹣3
﹣3![]() 等都是互为有理化因式,在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.
等都是互为有理化因式,在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.
例如:![]() ;
; ;
;
解答下列问题:
(1)3﹣![]() 与 互为有理化因式,将
与 互为有理化因式,将![]() 分母有理化得 .
分母有理化得 .
(2)计算:2﹣![]() ;
;
(3)观察下面的变形规律并解决问题.
①![]() =
=![]() ﹣1,
﹣1,![]() =
=![]()
![]() ,
,![]() =
=![]() ,…,若n为正整数,请你猜想:
,…,若n为正整数,请你猜想:![]() = .
= .
②计算:(![]() +
+![]() +
+![]() +…+
+…+![]() )×(
)×(![]() +1).
+1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(﹣4,0),点C是y轴正半轴上的一点,且∠ACB=90°,AC=BC

(1)如图①,若点B在第四象限,C(0,2),求点B的坐标;
(2)如图②,若点B在第二象限,以OC为直角边在第一象限作等腰Rt△COF,连接BF,交y轴于点M,求CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们定义直线![]() 为抛物线
为抛物线![]() 、b、c为常数,
、b、c为常数,![]() 的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.

已知抛物线![]() 与其“梦想直线”交于A、B两点
与其“梦想直线”交于A、B两点![]() 点A在点B的左侧
点A在点B的左侧![]() ,与x轴负半轴交于点C.
,与x轴负半轴交于点C.
![]() 填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______;
填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______;
![]() 如图,点M为线段CB上一动点,将
如图,点M为线段CB上一动点,将![]() 以AM所在直线为对称轴翻折,点C的对称点为N,若
以AM所在直线为对称轴翻折,点C的对称点为N,若![]() 为该抛物线的“梦想三角形”,求点N的坐标;
为该抛物线的“梦想三角形”,求点N的坐标;
![]() 当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙二人同时从A地出发,沿同一条道路去B地,途中都使用两种不同的速度Vl与V2(Vl<V2),甲用一半的路程使用速度Vl、另一半的路程使用速度V2;乙用一半的时间使用速度Vl、另一半的时间使用速度V2;关于甲乙二人从A地到达B地的路程与时间的函数图象及关系,有图中4个不同的图示分析.其中横轴t表示时间,纵轴s表示路程,其中正确的图示分析为( )

A. 图(1) B. 图(1)或图(2) C. 图(3) D. 图(4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x、y的方程组![]() ,其中﹣3≤a≤1,给出下列结论:
,其中﹣3≤a≤1,给出下列结论:
①![]() 是方程组的解;
是方程组的解;
②当a=﹣2时,x+y=0;
③若y≤1,则1≤x≤4;
④若S=3x﹣y+2a,则S的最大值为11.
其中正确的有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发xmin后距出发点的距离为y m.图中折线表示小亮在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).

(1)A点所表示的实际意义是 ;![]() = ;
= ;
(2)求出AB所在直线的函数关系式;
(3)如果小刚上坡平均速度是小亮上坡平均速度
的一半,那么两人出发后多长时间第一次相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,连结CP并延长CP交AD于Q点.给出以下结论:
①四边形AECF为平行四边形;
②∠PBA=∠APQ;
③△FPC为等腰三角形;
④△APB≌△EPC.
其中正确结论的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com