
【题目】如图,小华剪了两条宽均为![]() 的纸条,交叉叠放在一起,且它们的交角为
的纸条,交叉叠放在一起,且它们的交角为![]() ,则它们重叠部分的面积为( )
,则它们重叠部分的面积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
过A作AE⊥BC于E,AF⊥CD于F,则AE=AF=![]() ,∠AEB=∠AFD=90°,求出四边形ABCD是平行四边形,证出△AEB≌△AFD,推出AB=AD,求出四边形ABCD是菱形,根据菱形的性质得出AB=BC,解直角三角形求出AB,根据菱形的面积公式求出即可.
,∠AEB=∠AFD=90°,求出四边形ABCD是平行四边形,证出△AEB≌△AFD,推出AB=AD,求出四边形ABCD是菱形,根据菱形的性质得出AB=BC,解直角三角形求出AB,根据菱形的面积公式求出即可.
过A作AE⊥BC于E,AF⊥CD于F,则AE=AF=![]() ,∠AEB=∠AFD=90°.
,∠AEB=∠AFD=90°.
∵AD∥BC,AB∥CD,∴四边形ABCD是平行四边形,∴∠ABE=∠ADF=60°.
在△AEB和△AFD中,∵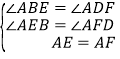 ,∴△AEB≌△AFD,∴AB=AD,∴四边形ABCD是菱形,∴AB=BC.
,∴△AEB≌△AFD,∴AB=AD,∴四边形ABCD是菱形,∴AB=BC.
在Rt△AEB中,∠AEB=90°,AE=![]() ,∠ABE=60°,∴BE=
,∠ABE=60°,∴BE=![]() =1,AB=
=1,AB=![]() =2,∴BC=AB=2,∴重叠部分的面积是BC×AE=2
=2,∴BC=AB=2,∴重叠部分的面积是BC×AE=2![]() .
.
故选D.


科目:初中数学 来源: 题型:
【题目】某学校为评估学生整理错题集的质量情况,进行了抽样调查,把学生整理错题集的质量分为“非常好”、“较好”、“一般”、“不好”四个等级,根据调查结果绘制了下面两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名学生;
(2)扇形统计图中,m= ,“非常好”部分所在扇形的圆心角度数为 ;
(3)补全条形统计图;
(4)如果4名学生整理错题集的质量情况是:3人“较好”,1人“一般”,现从中随机抽取2人,请用列表或画树状图的方法求出两人都是“较好”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂生产某种零件,每个零件的成本为40元,出厂单价为60元,该厂为鼓励销售商订购,制定了促销条件:当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元.
(1)若销售商一次订购x(x>100)个零件,直接写出零件的实际出厂单价y(元)?
(2)设销售商一次订购x(x>100)个零件时,工厂获得的利润为W元(W>0).
①求出W(元)与x(个)之间的函数关系式及自变量x的取值范围;并算出销售商一次订购多少个零件时,厂家可获得利润6000元;
②厂家为了达到既鼓励销售商订购又保证自己能获取最大利润的目的,重新制定新促销条件:在原有的基础上又增加了限制条件﹣﹣销售商订购的全部零件的实际出厂单价不能低于a(元).请你利用函数及其图象的性质求出a的值;并写出实行新促销条件时W(元)与x(个)之间的函数关系式及自变量x的取值范围.(工厂出售一个零件利润=实际出厂单价﹣每个零件的成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P,Q分别是等边△ABC边AB,BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ,CP交于点M.
(1)求证:△ABQ![]() △CAP;
△CAP;
(2)如图1,当点P,Q分别在AB,BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P,Q在分别运动到点B和点C后,继续在射线AB,BC上运动,直线AQ,CP交点为M,则∠QMC= 度.(直接填写度数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,动点
,动点![]() 从点
从点![]() 开始沿
开始沿![]() 以每秒
以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 移动,动点
移动,动点![]() 从点
从点![]() 开始沿
开始沿![]() 以每秒
以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 移动.如果
移动.如果![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,用
同时出发,用![]() (秒)表示移动的时间
(秒)表示移动的时间![]() ,那么:
,那么:
![]() 当
当![]() 为何值时,四边形
为何值时,四边形![]() 是梯形,此时梯形
是梯形,此时梯形![]() 的面积是多少?
的面积是多少?
![]() 当
当![]() 为何值时,以点
为何值时,以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
![]() 若设四边形
若设四边形![]() 的面积为
的面积为![]() ,试写出
,试写出![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 取何值时,四边形
取何值时,四边形![]() 的面积最小?
的面积最小?
![]() 在
在![]() 轴上是否存在点
轴上是否存在点![]() ,使点
,使点![]() 、
、![]() 在移动过程中,以
在移动过程中,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形的面积是一个常数?若存在请求出点
为顶点的四边形的面积是一个常数?若存在请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为美化校园,准备在长35米,宽20米的长方形场地上,修建若干条宽度相同的道路,余下部分作草坪,并请全校学生参与方案设计,现有3位同学各设计了一种方案,图纸分别如图l、图2和图3所示(阴影部分为草坪).

请你根据这一问题,在每种方案中都只列出方程不解.
①甲方案设计图纸为图l,设计草坪的总面积为600平方米.
②乙方案设计图纸为图2,设计草坪的总面积为600平方米.
③丙方案设计图纸为图3,设计草坪的总面积为540平方米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中AB=![]() ,BC=1,将矩形ABCD绕顶点B旋转得到矩形A'BC'D,点A恰好落在矩形ABCD的边CD上,则AD扫过的部分(即阴影部分)面积为( )
,BC=1,将矩形ABCD绕顶点B旋转得到矩形A'BC'D,点A恰好落在矩形ABCD的边CD上,则AD扫过的部分(即阴影部分)面积为( )
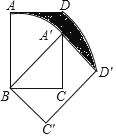
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com