
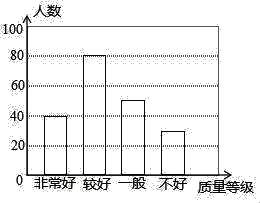
【题目】某学校为评估学生整理错题集的质量情况,进行了抽样调查,把学生整理错题集的质量分为“非常好”、“较好”、“一般”、“不好”四个等级,根据调查结果绘制了下面两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名学生;
(2)扇形统计图中,m= ,“非常好”部分所在扇形的圆心角度数为 ;
(3)补全条形统计图;
(4)如果4名学生整理错题集的质量情况是:3人“较好”,1人“一般”,现从中随机抽取2人,请用列表或画树状图的方法求出两人都是“较好”的概率.
【答案】(1)200;(2)40%;72°;(3)见解析;(4)![]() .
.
【解析】
(1)由“非常好”的人数和所占的百分比即可求出调查的 总人数;
(2)由“非常好”、“一般”、“不好”所占的百分比即可求出m的值;根据“非常好”所占的百分比即可求出“非常好”部分所在扇形的圆心角度数;
(3)分别求出“一般”、“不好”的人数即可补全条形统计图;
(4)画树状图展示所有12种等可能的结果数,再找出两人都是“较好”的结果数.然后根据概率公式求解;
解:(1)本次调查中,一共调查了40÷20%=200(人),
故答案为:200;
(2)扇形统计图中,m=1﹣20%﹣15%﹣25%=40%,“非常好”部分所在扇形的圆心角度数=20%×360°=72°,
故答案为:40%,72°;
(3)“一般”、“不好”的人数分别是200×25%=50(人),200×15%=30(人),
补全条形统计图如图所示:
(4)设3人“较好”,1人“一般”,分别为B,B,B,D,
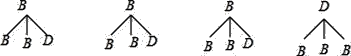
由树状图可知12种等可能的结果数,其中两人都是“较好”结果数为6,
所以两人都是“较好”的概率=![]() =
=![]() .
.


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】大学生小张利用暑假50天在一超市勤工俭学,被安排销售一款成本为40元/件的新型商品,此类新型商品在第x天的销售量p件与销售的天数x的关系如下表:
x(天) | 1 | 2 | 3 | … | 50 |
p(件) | 118 | 116 | 114 | … | 20 |
销售单价q(元/件)与x满足:当1≤x<25时q=x+60;当25≤x≤50时q=40+![]() .
.
(1)请分析表格中销售量p与x的关系,求出销售量p与x的函数关系.
(2)求该超市销售该新商品第x天获得的利润y元关于x的函数关系式.
(3)这50天中,该超市第几天获得利润最大?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:像(![]() +
+![]() )(
)(![]()
![]() )=3,
)=3,![]()
![]() =a(a≥0),(
=a(a≥0),(![]() +1)(
+1)(![]() ﹣1)=b﹣1(b≥0),……,这种两个含二次根式的代数式相乘,积不含二次根式,我们称这两个代数式互为有理化因式例如:
﹣1)=b﹣1(b≥0),……,这种两个含二次根式的代数式相乘,积不含二次根式,我们称这两个代数式互为有理化因式例如:![]() 与
与![]() ,
,![]() +1与
+1与![]() ﹣1,2
﹣1,2![]() +3
+3![]() 与2
与2![]() ﹣3
﹣3![]() 等都是互为有理化因式,在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.
等都是互为有理化因式,在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.
例如:![]() ;
; ;
;
解答下列问题:
(1)3﹣![]() 与 互为有理化因式,将
与 互为有理化因式,将![]() 分母有理化得 .
分母有理化得 .
(2)计算:2﹣![]() ;
;
(3)观察下面的变形规律并解决问题.
①![]() =
=![]() ﹣1,
﹣1,![]() =
=![]()
![]() ,
,![]() =
=![]() ,…,若n为正整数,请你猜想:
,…,若n为正整数,请你猜想:![]() = .
= .
②计算:(![]() +
+![]() +
+![]() +…+
+…+![]() )×(
)×(![]() +1).
+1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解
在⊙I中,弦AF与DE相交于点Q,则AQQF=DQQE.你可以利用这一性质解决问题.
问题解决
如图,在平面直角坐标系中,等边△ABC的边BC在x轴上,高AO在y轴的正半轴上,点Q(0,1)是等边△ABC的重心,过点Q的直线分别交边AB、AC于点D、E,直线DE绕点Q转动,设∠OQD=α(60°<α<120°),△ADE的外接圆⊙I交y轴正半轴于点F,连接EF.
(1)填空:AB= ;
(2)在直线DE绕点Q转动的过程中,猜想:![]() 与
与![]() 的值是否相等?试说明理由.
的值是否相等?试说明理由.
(3)①求证:AQ2=ADAE﹣DQQE;
②记AD=a,AE=b,DQ=m,QE=m(a、b、m、n均为正数),请直接写出mn的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AB=6,N为线段AB上的任意一点,∠BAC的平分线交BC于点D,M是AD上的动点, 连结BM、MN,则BM+MN的最小值是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市为方便行人过马路,打算修建一座高为4x(m)的过街天桥.已知天桥的斜面坡度i=1:0.75是指坡面的铅直高度DE(CF)与水平宽度AE(BF)的比,其中DC∥AB,CD=8x(m).
(1)请求出天桥总长和马路宽度AB的比;
(2)若某人从A地出发,横过马路直行(A→E→F→B)到达B地,平均速度是2.5m/s;返回时从天桥由BC→CD→DA到达A地,平均速度是1.5m/s,结果比去时多用了12.8s,请求出马路宽度AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(﹣4,0),点C是y轴正半轴上的一点,且∠ACB=90°,AC=BC

(1)如图①,若点B在第四象限,C(0,2),求点B的坐标;
(2)如图②,若点B在第二象限,以OC为直角边在第一象限作等腰Rt△COF,连接BF,交y轴于点M,求CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们定义直线![]() 为抛物线
为抛物线![]() 、b、c为常数,
、b、c为常数,![]() 的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.

已知抛物线![]() 与其“梦想直线”交于A、B两点
与其“梦想直线”交于A、B两点![]() 点A在点B的左侧
点A在点B的左侧![]() ,与x轴负半轴交于点C.
,与x轴负半轴交于点C.
![]() 填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______;
填空:该抛物线的“梦想直线”的解析式为______,点A的坐标为______,点B的坐标为______;
![]() 如图,点M为线段CB上一动点,将
如图,点M为线段CB上一动点,将![]() 以AM所在直线为对称轴翻折,点C的对称点为N,若
以AM所在直线为对称轴翻折,点C的对称点为N,若![]() 为该抛物线的“梦想三角形”,求点N的坐标;
为该抛物线的“梦想三角形”,求点N的坐标;
![]() 当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com