
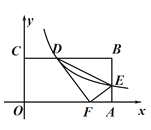
【题目】如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点B的坐标为(12,6),反比例函数![]() 的图象分别交边BC、AB于点D、E,连结DE,ΔDEF与ΔDEB关于直线DE对称.当点F正好落在边OA上时,则k的值为________.
的图象分别交边BC、AB于点D、E,连结DE,ΔDEF与ΔDEB关于直线DE对称.当点F正好落在边OA上时,则k的值为________.
【答案】27;
【解析】
如图,连接BF,过点D作DG⊥OA,垂足为G,用含k的代数式表示D,E的坐标,设F(x,0),求出直线DE、BF的斜率,根据两条垂直的直线的斜率相乘,乘积为﹣1求出x的值,证明△DGF∽△FAE,根据对应线段成比例列式求出k的值.
如图,连接BF,过点D作DG⊥OA,垂足为G,根据题意可知,D(![]() ,6),E(12,
,6),E(12,![]() ),∴直线DE的斜率k1=
),∴直线DE的斜率k1=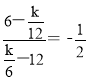 ,∵F在OA上,故可设F坐标为(x,0),∴直线BF的斜率k2=
,∵F在OA上,故可设F坐标为(x,0),∴直线BF的斜率k2=![]() ,∵ΔDEF与ΔDEB关于直线DE对称,∴BF⊥DE,∴k1k2=﹣1,即
,∵ΔDEF与ΔDEB关于直线DE对称,∴BF⊥DE,∴k1k2=﹣1,即![]() ,解得x=9,∴AF=3,∵∠OFE=90°+∠FEA=90°+∠DFG,∴∠DFG=∠FEA,又∵∠DGF=∠EAF=90°,∴△DGF∽△FAE,∴
,解得x=9,∴AF=3,∵∠OFE=90°+∠FEA=90°+∠DFG,∴∠DFG=∠FEA,又∵∠DGF=∠EAF=90°,∴△DGF∽△FAE,∴![]() ,即
,即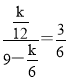 ,解得k=27.
,解得k=27.



科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC=3,点D在BC上且BD=2CD,E,F分别在AB,AC上运动且始终保持∠EDF=45°,设BE=x,CF=y,则y与x之间的函数关系用图象表示为:( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级(1)班全班50名同学组成五个不同的兴趣爱好小组,每人都参加且只能参加一个小组,统计(不完全)人数如下表:
编号 | 一 | 二 | 三 | 四 | 五 |
人数 |
| 15 | 20 | 10 |
|
已知前面两个小组的人数之比是![]() .
.
解答下列问题:
(1)![]() .
.
(2)补全条形统计图:
(3)若从第一组和第五组中任选两名同学,求这两名同学是同一组的概率.(用树状图或列表把所有可能都列出来)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了4米(BB′),再把竹竿竖立在地面上,测得竹竿的影长(B′C′)为1.8米,求路灯离地面的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
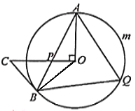
【题目】如图,AB是⊙O的弦,过点O作OC⊥OA,OC交于AB于P,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)已知∠BAO=25°,点Q是弧AmB上的一点.
①求∠AQB的度数;
②若OA=18,求弧AmB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(发现)如图,点E,F分别在正方形ABCD的边BC,CD上,连接EF.因为AB=AD,所以把ΔABE绕A逆时针旋转90°至ΔADG,可使AB与AD重合.因为∠CDA=∠B=90°,所以∠FDG=180°,所以F、D、G共线.
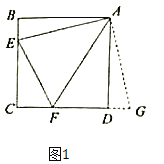
如果__________(填一个条件),可得ΔAEF≌ΔAGF.经过进一步研究我们可以发现:当BE,EF,FD满足__________时,∠EAF=45°.
(应用)
如图,在矩形ABCD中,AB=6,AD=m,点E在边BC上,且BE=2.
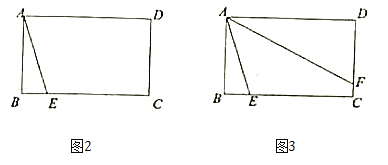
(1)若m=8,点F在边DC上,且∠EAF=45°(如图),求DF的长;
(2)若点F在边DC上,且∠EAF=45°,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台在它的娱乐性节目中每期抽出两名场外幸运观众,有一期甲、乙两人被抽为场外幸运观众,他们获得了一次抽奖的机会,在如图所示的翻奖牌的正面4个数字中任选一个,选中后翻开,可以得到该数字反面的奖品,第一个人选中的数字第二个人不能再选择了.
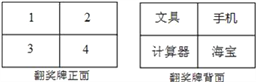
(1)如果甲先抽奖,那么甲获得“手机”的概率是多少?
(2)小亮同学说:甲先抽奖,乙后抽奖,甲、乙两人获得“手机”的概率不同,且甲获得“手机”的概率更大些.你同意小亮同学的说法吗?为什么?请用列表或画树状图分析.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com