
如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,过点C作CF∥BE交DE的延长线于F.
(1)求证:四边形BCFE是菱形;
(2)若 ,求菱形BCFE的面积.
,求菱形BCFE的面积.

(1)证明见解析;(2) .
.
【解析】
试题分析:(1)从所给的条件可知,DE是△ABC中位线,所以DE∥BC且2DE=BC,所以BC和EF平行且相等,所以四边形BCFE是平行四边形,又因为BE=FE,所以四边形BCFE是菱形.
(2)因为∠BCF=120°,所以∠EBC=60°,所以菱形的边长也为4,求出菱形的高面积就可求.
(1)∵D、E分别是AB、AC的中点,∴DE∥BC且2DE=BC.
又∵BE=2DE,EF=BE,∴EF=BC,EF∥BC.
∴四边形BCFE是平行四边形.
又∵BE=FE,∴四边形BCFE是菱形.
(2)∵∠BCF=120°,∴∠EBC=60°.
∴△EBC是等边三角形.
∴菱形的边长为4,高为 .
.
∴菱形的面积为4× =
= .
.
考点:1.菱形的判定和性质;2.三角形中位线定理;3.等边三角形的判定和性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2013-2014学年吉林省长春市朝阳区中考一模数学试卷(解析版) 题型:解答题
如图①,在平面直角坐标系中,点A是抛物线y=x2在第一象限上的一个点,连结OA,过点A作AB⊥OA,交y轴于点B,设点A的横坐标为n.
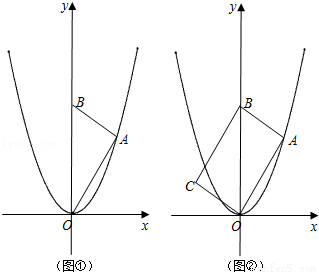
【探究】:
(1)当n=1时,点B的纵坐标是 ;
(2)当n=2时,点B的纵坐标是 ;
(3)点B的纵坐标是 (用含n的代数式表示).
【应用】:
如图②,将△OAB绕着斜边OB的中点顺时针旋转180°,得到△BCO.
(1)求点C的坐标(用含n的代数式表示);
(2)当点A在抛物线上运动时,点C也随之运动.当1≤n≤5时,线段OC扫过的图形的面积是 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年吉林省长春市朝阳区中考一模数学试卷(解析版) 题型:选择题
如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=50°,∠1=35°,则∠2的度数为( )

A.35° B.65° C.85° D.95°
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市顺义区中考二模数学试卷(解析版) 题型:解答题
在△ABC中, AB=AC ,∠A=300,将线段 BC 绕点 B 逆时针旋转 600得到线段 BD ,再将线段BD平移到EF,使点E在AB上,点F在AC上.
(1)如图 1,直接写出∠ABD和∠CFE的度数;
(2)在图1中证明:AE =CF;
(3)如图2,连接 CE ,判断△CEF的形状并加以证明.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市顺义区中考二模数学试卷(解析版) 题型:选择题
陈老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同.由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格(单位:元)为( )

A.19 B.18 C.16 D.15
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市顺义区中考一模数学试卷(解析版) 题型:解答题
已知:如图,E是AC上一点,AB=CE,AB∥CD,∠ACB =∠D.求证:BC =ED.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com