
【题目】如图,在同一平面内有三点A、B、C.
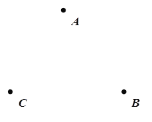
(1)作射线CA,连接BC;
(2)延长线段BC,得到射线CD,画∠ACD平分线CE;
(3)在射线CD上取一点F,使得CF = AC;
(4)在射线CE上作一点P,使PF + PA最小;
(5)第(4)步作图的依据是 .
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
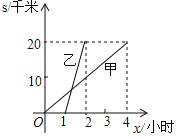
【题目】已知A、B两地之间的距离为20千米,甲步行,乙骑车,两人沿着相同路线,由A地到B地匀速前行,甲、乙行进的路程s与x(小时)的函数图象如图所示.(1)乙比甲晚出发___小时;(2)在整个运动过程中,甲、乙两人之间的距离随x的增大而增大时,x的取值范围是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
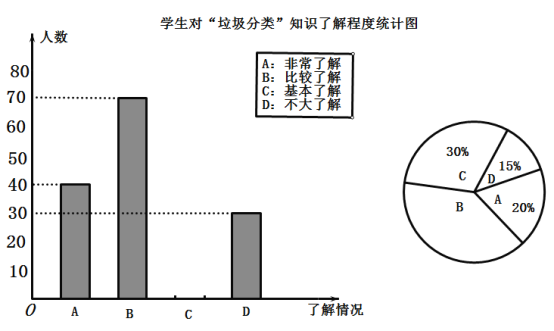
月![]() 日,我市在政府广场举行垃圾分类启动仪式,引导市民正确分类投放垃圾,提高大家环保意识,倡导文明习惯,为调查学生对“垃圾分类”知识的了解程度,玲玲所在的课外小组对本校同学进行了一次随机问卷调查,并将统计的结果绘制了两幅不完整的统计图,请根据图中的信息解答下列问题:
日,我市在政府广场举行垃圾分类启动仪式,引导市民正确分类投放垃圾,提高大家环保意识,倡导文明习惯,为调查学生对“垃圾分类”知识的了解程度,玲玲所在的课外小组对本校同学进行了一次随机问卷调查,并将统计的结果绘制了两幅不完整的统计图,请根据图中的信息解答下列问题:
(1)本次调查共调查了 人,“比较了解”所占扇形统计图圆心角的度数为 ;
(2)请将两个统计图补充完整;
(3)若玲玲所在的学校有![]() 人,请你估计一下“非常了解”和“比较了解”大约共有多少人?
人,请你估计一下“非常了解”和“比较了解”大约共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场准备进一批两种不同型号的衣服,已知购进A种型号衣服9件,B种型号衣服10件,则共需1810元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知销售一件A型号衣服可获利18元,销售一件B型号衣服可获利30元,要使在这次销售中获利不少于699元,且A型号衣服不多于28件.
(1)求A、B型号衣服进价各是多少元?
(2)若已知购进A型号衣服是B型号衣服的2倍还多4件,则商店在这次进货中可有几种方案并简述购货方案.
【答案】(1)A种型号的衣服每件90元,B种型号的衣服100元;(2)有三种进货方案,具体见解析.
【解析】试题分析:(1)等量关系为:A种型号衣服9件×进价+B种型号衣服10件×进价=1810,A种型号衣服12件×进价+B种型号衣服8件×进价=1880;
(2)关键描述语是:获利不少于699元,且A型号衣服不多于28件.关系式为:18×A型件数+30×B型件数≥699,A型号衣服件数≤28.
试题解析:(1)设A种型号的衣服每件x元,B种型号的衣服y元,
则:![]() ,
,
解之得![]() .
.
答:A种型号的衣服每件90元,B种型号的衣服100元;
(2)设B型号衣服购进m件,则A型号衣服购进(2m+4)件,
可得:![]() ,
,
解之得192m12,
∵m为正整数,
∴m=10、11、12,2m+4=24、26、28.
答:有三种进货方案:
(1)B型号衣服购买10件,A型号衣服购进24件;
(2)B型号衣服购买11件,A型号衣服购进26件;
(3)B型号衣服购买12件,A型号衣服购进28件。
点睛:点睛:本题主要考查二元一次方程组和一元一次不等式组的实际问题的应用,解题的关键是读懂题目的意思,根据题目给出的条件,设出未知数,分别找出甲组和乙组对应的工作时间,找出合适的等量关系,列出方程组,再求解.
【题型】解答题
【结束】
21
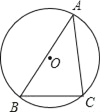
【题目】如图,锐角△ABC内接于⊙O,若⊙O的半径为6,sinA=![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某项工程由甲乙两队合作12天可以完成,供需工程费用13800元,乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的1.5倍,且甲队每天的工程费用比乙队多150元。
(1)甲乙两队单独完成这项工程分别需要多少天?
(2)若工程管理部门决定从这两个队中选一个队单独完成这项工程,从节约资金的角度考虑,应该选择哪个工程队?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,OC是∠AOB的平分线.
(1)当∠AOB = 60°时,求∠AOC的度数;
(2)在(1)的条件下,过点O作OE⊥OC,补全图形,并求∠AOE的度数;
(3)当∠AOB =![]() 时,过点O作OE⊥OC,直接写出∠AOE的度数(用含
时,过点O作OE⊥OC,直接写出∠AOE的度数(用含![]() 代数式表示).
代数式表示).
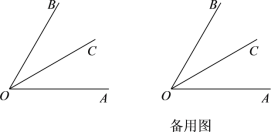
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个,七年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行调查,根据调查结果绘制成如下两幅不完整的统计图.

(1)求共抽取了多少名学生的征文;
(2)将上面的条形统计图补充完整;
(3)在扇形统计图中,“爱国”主题所对应的圆心角是多少;
(4)如果该校七年级共有![]() 名学生,请估计该校选择以“友善”为主题的七年级学生有多少名.
名学生,请估计该校选择以“友善”为主题的七年级学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】〖定义〗:若关于![]() 的一元一次方程
的一元一次方程![]() 的解恰好为
的解恰好为![]() 即
即![]() ,则称该方程为“友好方程”.例如:方程
,则称该方程为“友好方程”.例如:方程![]() 的解为
的解为![]() ,而
,而![]() ,则方程
,则方程![]() 为“友好方程”.
为“友好方程”.
〖运用〗:(1)①![]() ,②
,②![]() ③
③![]() 三个方程中,为“友好方程”的是______(填写序号)
三个方程中,为“友好方程”的是______(填写序号)
(2)若关于![]() 的一元一次方程
的一元一次方程![]() 是“友好方程”,求
是“友好方程”,求![]() 的值;
的值;
(3)若关于![]() 的一元一次方程
的一元一次方程![]() 是“友好方程”,求
是“友好方程”,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人玩“石头、剪刀、布”游戏,他们在不透明的袋子中放入形状、大小均相同的12张卡片,其中写有“石头”“剪刀”“布”的卡片张数分别为3、4、5,两人各随机摸出一张卡片(先摸者不放回卡片)来比胜负,并约定:“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,但同种卡片不分胜负.
(1)若甲先摸,则他摸出“石头”的概率是多少?
(2)若甲先摸出“石头”,则乙获胜的概率是多少?
(3)若甲先摸,则他摸出哪种卡片获胜的可能性最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com