
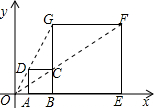
 如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为$\frac{1}{3}$.点A、B、E在x轴上,若正方形BEFG的边长为6,则C点坐标为(3,2).
如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为$\frac{1}{3}$.点A、B、E在x轴上,若正方形BEFG的边长为6,则C点坐标为(3,2). 分析 先利用位似的性质得到$\frac{BC}{6}$=$\frac{OB}{OB+6}$=$\frac{1}{3}$,然后利用比例性质求出BC和OB即可得到C点坐标.
解答 解:∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且位似比为$\frac{1}{3}$.
∴$\frac{BC}{EF}$=$\frac{OB}{OE}$=$\frac{1}{3}$,
而BE=EF=6,
∴$\frac{BC}{6}$=$\frac{OB}{OB+6}$=$\frac{1}{3}$,
∴BC=2,OB=3,
∴C(3,2).
故答案为(3,2)
点评 本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2017届江苏省扬州市九年级下学期第一次月考数学试卷(解析版) 题型:填空题
反比例函数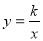 的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为 .
的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
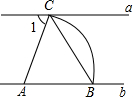 如图,直线a∥b,点A在直线b上,以点A为圆心,适当长为半径画弧,分别交直线a、b于C、B两点,连接AC、BC,若∠ABC=54°,则∠1的大小为( )
如图,直线a∥b,点A在直线b上,以点A为圆心,适当长为半径画弧,分别交直线a、b于C、B两点,连接AC、BC,若∠ABC=54°,则∠1的大小为( )| A. | 36° | B. | 54° | C. | 72° | D. | 63° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com