
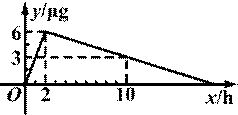
某医药研究所开发一种新药.在试验药效时发现,如果成人按规定剂量服用,那么服药2h后血液中含药量最高,达到每毫升6μg(1μg=10-3mg),接着逐步衰减,10h后血液中含药量为每毫升3μg.若每毫升血液中含药量y(μg)随时间x(h)的变化如图所示,则当成人按规定剂量服药后:
(1)当0≤x≤2时,y=3x.
②当x>2时, 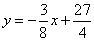 .
.
(2)有效时间是6h.
【解析】(1)根据图象写出函数解析式,前面2h对应的线段是正比例函数的图象,设为y=k1x(k1≠0),把(2,6)代入即可求出k1.当x>2时,图象对应的是一次函数,设为y=k2x+b(k2≠0).把(2,6),(10,3)代入即可求出k2,b.(2)由图象可知,有两个时刻成人血液中的含药量为4μg,这两个时刻间的时间段内含药量高于4μg.
解:(1)根据图象可知,当0≤x≤2时,y是x的正比例函数;当x>2时,y是x的一次函数.
①当0≤x≤2时,设y=k1x(k1≠0),把(2,6)代入y=k1x,得k1=3.
所以当0≤x≤2时,y=3x.
②当x>2时,设y=k2x+b(k2≠0),把(2,6),(10,3)代入y=k2x+b中,得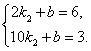 解得
解得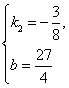
所以当x>2时,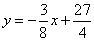 .
.
(2)把y=4代入y=3x,得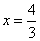 ;把y=4代入
;把y=4代入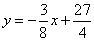 ,得
,得 .因为
.因为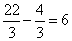 ,所以这个有效时间是6h.
,所以这个有效时间是6h.
【难度】一般


科目:初中数学 来源: 题型:
在平面直角坐标系中,将坐标为(-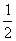 ,
,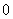 ),(-
),(-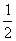 ,1),(-3
,1),(-3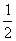 ,1),(-1
,1),(-1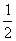 ,3),(-
,3),(-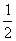 ,6),(-1,6),(0,8),(1,6),(
,6),(-1,6),(0,8),(1,6),(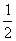 ,6),(2
,6),(2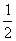 ,3),(1
,3),(1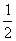 ,3),(3
,3),(3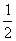 ,1),(
,1),(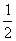 ,1),(
,1),(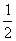 ,0)的点,顺次用线段连起来,并将最后一点与第一点连起来形成一个图形,说一说该图形是一个什么图形?
,0)的点,顺次用线段连起来,并将最后一点与第一点连起来形成一个图形,说一说该图形是一个什么图形?
查看答案和解析>>
科目:初中数学 来源: 题型:
已知一次函数y=kx+b的图象经过点(-1,-5),且与正比例函数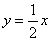 的图象相交于点(2,a).
的图象相交于点(2,a).
(1)求a的值.
(2)求一次函数y=kx+b的表达式.
(3)在同一坐标系中,画出这两个函数的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
某景区内的环形路是边长为800米的正方形 ABCD,如图1和图2.现有1号、2号两游览车分别从出口A和景点C同时出发,1号车顺时针、2号车逆时针沿环形路连续循环行驶.供游客随时免费乘车(上、下车的时间忽略不计),两车速度均为200米/分.
ABCD,如图1和图2.现有1号、2号两游览车分别从出口A和景点C同时出发,1号车顺时针、2号车逆时针沿环形路连续循环行驶.供游客随时免费乘车(上、下车的时间忽略不计),两车速度均为200米/分.
探究
设行驶时间为t分.

(1)当0≤t≤8时,分别写出1号车、2号车在左半环线离出口A的路程y1,y2(米)与t(分)的函数关系式,并求出当两车相距的路程是400米时t的值;
(2)t为何值时,1号车第三次恰好经过景点C?并直接写出这一段时间内它与2号车相遇过的次数.
发现
如图2,游客甲在BC上的一点K(不与点B,C重合)处候车,准备乘车到出口A.设CK=x米.
情况一:若他刚好错过2号车,便搭乘即将到来的1号车;
情况二:若他刚好错过1号车,便搭乘即将到来的2号车.
比较哪种情况用时较多.(含候车时间)决策
已知游客乙在DA上从D向出口A走去,步行的速度是50米/分.当行进到DA上一点P(不与点D,A重合)时,刚好与2号车迎面相遇.
(1)他发现,乘1号车会比乘2号车到出口A用时少,请你简要说明理由;
(2)设PA=s(0<s<800)米.若他想尽快到达出口A,根据s的大小,在等候乘1号车还是步行这两种方式中,他该如何选择?
查看答案和解析>>
科目:初中数学 来源: 题型:
如下图,过正方形ABCD的顶点B作直线l,过点A,C作直线l的垂线,垂足分别为E,F,直线AE交CD于点G.
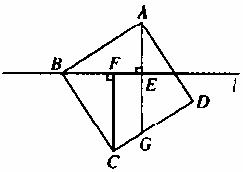

(1)求证:△ABE≌△BCF;
(2)若∠CBF=65°,求∠AGC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com