
如下图,过正方形ABCD的顶点B作直线l,过点A,C作直线l的垂线,垂足分别为E,F,直线AE交CD于点G.
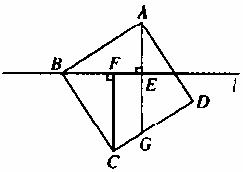

(1)求证:△ABE≌△BCF;
(2)若∠CBF=65°,求∠AGC的度数.
1)证明:∵正方形ABCD,

∴AB=CB,∠ABC=90°
∵AE 于点E,
于点E,
∴∠ABE+∠BAE=90°,
∴∠BAE=∠CBF.
又∵∠AEB=∠BFC=90°,
∴△ABE≌△BCF(AAS).
(2)115°.
【解析】
试题分析:(1)根据正方形的性质,易得△ABE与△BCF的两角与一条边相等,利用全等三角形的判定条件AAS,可证明两三角形全等;(2)根据△ABE≌△BCF,又知∠CBF=65°,可得∠BAE=65°,又由正方形的性质可得AB∥DC,即可得出∠AGC的度数.
试题解析:解:(1)证明:∵正方形ABCD,


∴AB=CB,∠ABC=90°
∵AE 于点E,
于点E,
∴∠ABE+∠BAE=90°,
∴∠BAE=∠CBF.
又∵∠AEB=∠BFC=90°,
∴△ABE≌△ BCF(AAS).
BCF(AAS).
(2)∵△ABE≌△BCF,∠CBF=65°,
∴∠BAE=65°,
又由正方形ABCD得AB∥DC,
∴∠AGC=180°-65°=115°.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
设点A的坐标(x,y),其中横坐标x可取-1,2,纵坐标y可取-1,1,2。
(1)求出点A的坐标的所有等可能结果(用树形图或列表法求解);
(2)求点A与点B(1,-1)关于原点对称的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
观察下列等式:
①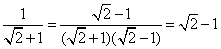 ;
;
②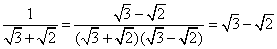 ;
;
③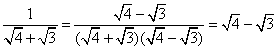 ;
;
……
回答下列问题:
(1)仿照上列等式,写出第n个等式: ;
(2)利用你观察到的规律,化简: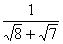 ;
;
(3)计算: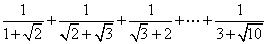 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
某医药研究所开发一种新药.在试验药效时发现,如果成人按规定剂量服用,那么服药2h后血液中含药量最高,达到每毫升6μg(1μg=10-3mg),接着逐步衰减,10h后血液中含药量为每毫升3μg.若每毫升血液中含药量y(μg)随时间x(h)的变化如图所示,则当成人按规定剂量服药后:
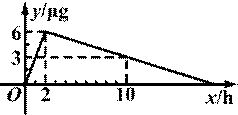
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
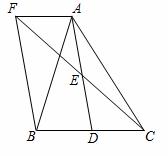

(1)求证:D是BC的中点;
(2)如果AB=AC,试判断四边形AFBD是什么四边形,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com