
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
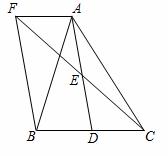

(1)求证:D是BC的中点;
(2)如果AB=AC,试判断四边形AFBD是什么四边形,并证明你的结论.
(1)∵AF∥BC,∴∠EAF=∠EDC,∵E是AD的中点,∴AE=DE,在△EAF和△EDC中,∵∠EAF=∠EDC,AE=DE,∠AEF=∠DEC,∴△EAF≌△EDC(ASA),∴DC=AF,又∵AF=BD,∴BD=DC,∴D是BC的中点;
(2)矩形,理由是:
∵AF∥BD,AF=BD,∴四边形AFBD是平行四边形
∵AB=AC,D是BC的中点,∴AD⊥BC,∴∠ADB=90°,
∴四边形AFBD是矩形.
【解析】
试题分析:(1)利用△AEF≌△DEC来证;
(2)利用一组对边平行且相等的四边形是平行四边形,得出四边形AFBD是平行四边形,进而得出四边形AFBD是矩形.
试题解析:(1)∵AF∥BC,∴∠EAF=∠EDC,∵E是AD的中点,∴AE=DE,在△EAF和△EDC中,∵∠EAF=∠EDC,AE=DE,∠AEF=∠DEC,∴△EAF≌△EDC(ASA),∴DC=AF,又∵AF=BD,∴BD=DC,∴D是BC的中点;
(2)四边形AFBD是矩形.理由是:
∵AF∥BD,AF=BD,∴四边形AFBD是平行四边形
∵AB=AC,D是BC的中点,∴AD⊥BC,∴∠ADB=90°,
∴四边形AFBD是矩形.
【难度】一般


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:
 已知:如
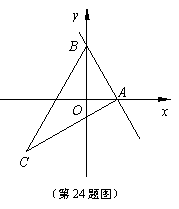
已知:如 图,直线y=kx+2与x轴的正半轴相交于点A(t,0)、与y轴相交于点B,抛物线
图,直线y=kx+2与x轴的正半轴相交于点A(t,0)、与y轴相交于点B,抛物线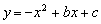 经过点A和点B,点C在第三象限内,且AC⊥AB,tan∠ACB=
经过点A和点B,点C在第三象限内,且AC⊥AB,tan∠ACB=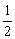 .
.
(1)当t=1时,求抛物线的表达式;
(2)试用含t的代数式表示点C的坐标;
(3)如果点C在这条抛物线的对称轴上,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
A、B两个火车站相距360km.一列快车与一列普通列车分别从A,B两站同时出发相向而行,快车的速度比普通列车的速度快54km/h,当快车到达B站时, 普通列车距离A站还有135km.求快车和普通列车的速度各是多少?
普通列车距离A站还有135km.求快车和普通列车的速度各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
某校举办了一次知识竞赛,满分10分,学生得分均为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包括9分)为优秀.这次竞赛中甲、乙两组学生成绩分布的条形统计图如图所示.
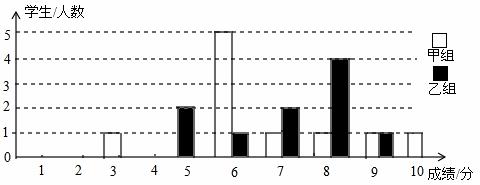
(1)补充完成下面的成绩统计分析表:

(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组,请你给出两条支持乙组同学观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如下图,过正方形ABCD的顶点B作直线l,过点A,C作直线l的垂线,垂足分别为E,F,直线AE交CD于点G.
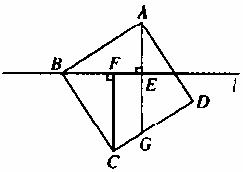

(1)求证:△ABE≌△BCF;
(2)若∠CBF=65°,求∠AGC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,
 ABCD中,点E、F在BD上,且BF=DE.
ABCD中,点E、F在BD上,且BF=DE.
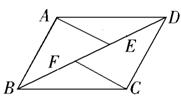

(1)写出图中所有你认为全等的三角形;
(2)延长AE交BC的延长线于G,延长CF交DA的延长线于H(请补全图形),证明四边形AGCH是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com