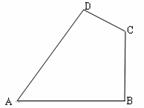
如图，已知在四边形ABCD中，AB＝20cm，BC＝15 cm，CD＝7 cm，AD＝24 cm，∠ABC＝90°。猜想∠A与∠C关系并加以证明.
科目：初中数学 来源： 题型：
把一张边长为40 cm的正方形硬纸板，进行适当的裁剪，折成一个长方体盒子（纸板的厚度忽略不计）．
（1）如图，若在正方形硬纸板的四角各剪掉一个同样大小的正方形，将剩余
部分折成一个无盖的长方体盒子．
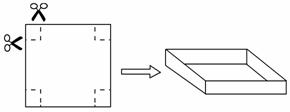
①要使折成的长方体盒子的底面积为484 cm2，那么剪掉的正方形的边长为多少？
②折成的长方体盒子的侧面积是否有最大值？如果有，求出这个最大值和此时剪掉的正方形的边长；如果没有，说明理由．
（2）若在正方形硬纸板的四周剪掉一些矩形（即剪掉的矩形至少有一条边在正方形硬纸板的边上），将剩余部分折成一个有盖的长方体盒子．若折成的一个长方体盒子的表面积为550 cm2，求此时长方体盒子的长、宽、高（只需求出符合要求的一种情况）．
查看答案和解析>>
科目：初中数学 来源： 题型：
某楼盘一楼是车库（暂不销售），二楼至二十三楼均为商品房（对外销售）．商品房售价方案如下：第八层售价为3000元/米2，从第八层起每上升一层，每平方米的售价增加40元；反之，楼层每下降一层，每平方米的售价减少20元．已知商品房每套面积均为120平方米．开发商为购买者制定了两种购房方案：
方案一：购买者先交纳首付金额（商品房总价的30％），再办理分期付款（即贷款）．
方案二：购买者若一次付清所有房款，则享受8％的优惠，并免收五年物业管理费（已知每月物业管理费为a元）
（1）请写出每平方米售价y（元/米2）与楼层x（2≤x≤23，x是正整数）之间的函数解析式；
（2）小张已筹到120000元，若用方案一购房，他可以购买哪些楼层的商品房呢？
（3）有人建议老王使用方案二购买第十六层，但他认为此方案还不如不免收物业管理费而直接享受9％的优惠划算．你认为老王的说法一定正确吗？请用具体的数据阐明你的看法．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交CE的延长线于点F，且AF＝BD，连接BF．
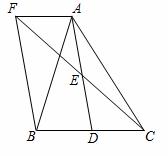
（1）求证：D是BC的中点；
（2）如果AB＝AC，试判断四边形AFBD是什么四边形，并证明你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
已知：在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B、C重合）．以AD为边作正方形ADEF，连接CF．
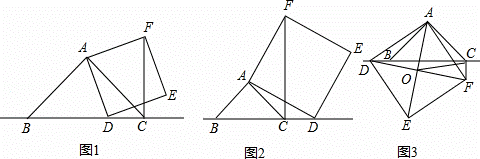
（1）如图1，当点D在线段BC上时，求证：①BD⊥CF．②CF=BC﹣CD．
（2）如图2，当点D在线段BC的延长线上时，其它条件不变，请直接写出CF、BC、CD三条线段之间的关系；
（3）如图3，当点D在线段BC的反向延长线上时，且点A、F分别在直线BC的两侧，其它条件不变：①请直接写出CF、BC、CD三条线段之间的关系．②若连接正方形对角线AE、DF，交点为O，连接OC，探究△AOC的形状，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图①所示，在正方形ABCD中，M是AB的中点，E是AB的延长线上一点，MN⊥DM，且交∠CBE的平分线于点N．
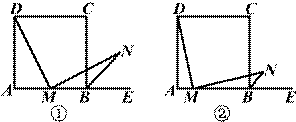
（1）求证：MD＝MN；
（2）若将上述条件中“M是AB的中点”改成“M是AB上任意一点”，其余条件不变，如图②所示，则结论“MD＝MN”还成立吗？若成立，给出证明；若不成立，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
中，函数值
随
的增大而 .
．
，AD=4，将平行四边形ABCD沿AE翻折后，点B恰好与点C重合，则折痕AE的长为 ．