
����Ŀ���������
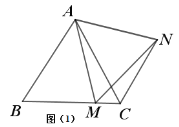
��1����ͼ��1�����ڵȱ�������ABC�У���M��BC�ϵ�����һ�㣨�����˵�B��C��������AM����AMΪ�����ȱ�������AMN������CN�����ACN�� �㣮
���̽��
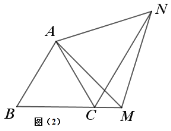
��2����ͼ��2�����ڵȱ�������ABC�У���M��BC�ӳ����ϵ�����һ�㣨�����˵�C���������������䣬��1���еĽ��ۻ���������˵�����ɣ�
��չ����
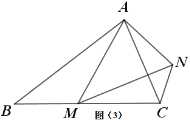
��3����ͼ��3�����ڵ���������ABC�У�BA��BC����M��BC�ϵ�����һ�㣨�����˵�B��C��������AM����AMΪ��������������AMN��ʹAM��MN������CN������һ��������ʹ�á�ABC����ACN�Գ�����д���������ӵ���������˵�����ɣ�
���𰸡���1��60����2������������3��������
��������
��1�����ݵȱ������ε����ʿɵ�AB=AC��AM=AN����BAC=��MAN=60���������õ���BAM=��CAN��������SAS��֤��![]() ��
��![]() ���̶��ó����ۣ�
���̶��ó����ۣ�
��2��Ҳ����ͨ��֤��![]() ��
��![]() ���ó����ۣ��ͣ�1����˼·��ȫһ����
���ó����ۣ��ͣ�1����˼·��ȫһ����
��3������ABC����AMNʱ��![]() ��
��![]() ���������Ƶ����ʵõ�
���������Ƶ����ʵõ�![]() ���ָ��ݡ�BAM����CAN��֤��
���ָ��ݡ�BAM����CAN��֤��![]() ��
��![]() �����ɵõ��𰸣�
�����ɵõ��𰸣�
��1��֤������![]() ��
��![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��AB=AC��AM=AN����BAC=��MAN=60����
���BAM=��CAN��
����![]() ��
��![]() ��
�У�
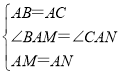 ��
��
��![]() ��
��![]() ��SAS����
��SAS����
���ABC=��ACN��
��![]() �ǵȱ�������
�ǵȱ�������
���ABC=60��
���ACN=��ABC=60����
��2�����ۡ�ACN��60���Գ�����
�������£���![]() ��
��![]() ���ǵȱ������Σ�
���ǵȱ������Σ�
��AB��AC��AM��AN����BAC����MAN��60����
���BAM����CAN��
��![]() ��
��![]() ��
��
���ACN����ABM��60����
��3��������������ABC����AMN��
�������£�
��BA��BC��MA��MN����ABC����AMN��
���BAC����MAN��
��![]() ��
��![]() ��
��
��![]() ��
��
�֡�BAM����BAC����MAC����CAN����MAN����MAC��
���BAM����CAN��
��![]() ��
��![]() ��
��
���ABC����ACN��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
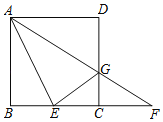
����Ŀ����ͼ����������ABCD�У���E��BC���ϣ�����AE����DAE��ƽ����AG��CD�߽��ڵ�G����BC���ӳ��߽��ڵ�F����![]() ����������0����
����������0����
��1����AB��2������1�����߶�CF�ij���
��2������EG����EG��AF��
����֤����GΪCD�ߵ��е㣮
��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�Ծ���һ��50��ѧ�����г�����Ŀ�IJ��ԣ����ݲ��Գɼ�����������ͳ��ͼ.

����������Ϣ������������⣺
��1�����β��Ե�ѧ���У���3�ֵ�ѧ����________�ˣ���4�ֵ�ѧ����________�ˣ�
��2������50�����ݵ�ƽ��������������λ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2022�걱�����»Ἢ������նա�����èΪԭ�ͽ�����ƴ������������а»Ἢ���ѩ���ڡ������й���־�Է��ŵĵ���Ϊ���������ƴ��������նա��͡�ѩ���ڡ���һ���dz������Ĵ�����ϣ����й��Ļ��Ͱ���ƥ�˾�����һ�������Ľ�������С����նա��͡�ѩ���ڡ��ļ�����Ʊ��2�ţ���ͼ������4����Ʊ������ȫ��ͬ�������������С�ú�С������һ�ż�����Ʊ��������С�ô���4����Ʊ�������ȡһ�ţ�Ȼ������С����ʣ�µ�3���������ȡһ��.

��1��С�ó鵽�����նա��ļ�����Ʊ�ĸ�����__________��
��2��������״ͼ���б�����С�ú�С�����鵽��ѩ���ڡ��ļ�����Ʊ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͣ�β�ͣѧ��ѧϰ�����ڣ���ij�н�����Ϊ�˽����ѧ�������ڼ��ڼ�ѧϰʱ��һЩѧϰ��ʽ��ϲ�������ͨ���Ų��õ����ʾ��ķ�ʽ��������˲���ѧ�������ӵ������ͼ��ʾ���������ݵ����������������в�������ͳ��ͼ��
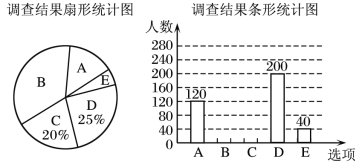
��������ͳ��ͼ������������⣺
��1�����ν��ܵ����ѧ������ �ˣ�
��2����ȫ����ͳ��ͼ��
��3������ͳ��ͼ�У�����B��Բ�ĽǵĶ����� �ȣ�
��4��������Լ��16��������������ϲ����ѧ��ѡ��ѡ��C��D����ѧ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() Ϊƽ���ı���
Ϊƽ���ı���![]() ��
��![]() ��һ�㣬��
��һ�㣬��![]() ��
��![]() ���۵õ�
���۵õ�![]() �� ��
�� ��![]() ��
��![]() �ϣ���
�ϣ���![]() ����
����![]() ����
����![]() __________��
__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ 1��ֱ��![]() ��
��![]() �ᣬ
�ᣬ![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ����
����![]() ��������
��������![]() ������
������![]() ����
����![]() �͵�
�͵�![]() ������ֱ��
������ֱ��![]() ������һ��
������һ��![]() ��
��
��1����������![]() �Ľ���ʽ��
�Ľ���ʽ��
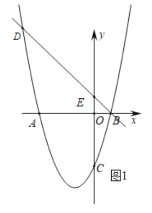
��2����ͼ 2����![]() Ϊ
Ϊ![]() ����һ���㣬����
����һ���㣬����![]() ����
����![]() ʱ�����
ʱ����� ![]() �����ꣻ
�����ꣻ
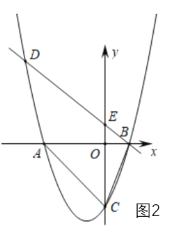
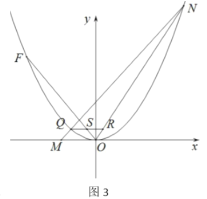
��3����ͼ 3����������![]() ƽ�ƣ�ʹ�䶥��������ԭ��
ƽ�ƣ�ʹ�䶥��������ԭ��![]() ���õ�������
���õ�������![]() ����ֱ��
����ֱ��![]() ����ƽ�ƾ�������ԭ��
����ƽ�ƾ�������ԭ��![]() ����������
����������![]() ����һ��
����һ��![]() ����
����![]() ����
����![]() ��
��![]() ����λ�� ��һ������һ���㣬
����λ�� ��һ������һ���㣬![]() ��
��![]() ��
��![]() �㣬
�㣬![]() ��ֱ�
��ֱ�![]() ��
��![]() ����˵����
����˵����![]() ��
��![]() ����һ��ȷ����������ϵ��
����һ��ȷ����������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
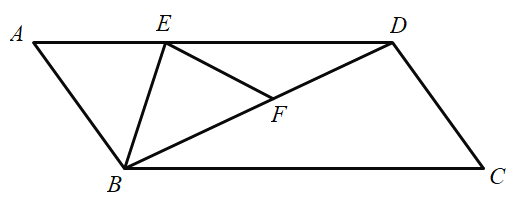
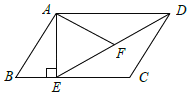
����Ŀ����ͼ����ƽ���ı���ABCD�У�����A��AE��BC������ΪE������DE��FΪ�߶�DE��һ�㣬����AFE����B��
��1����֤����ADF�ס�DEC��
��2����AB��8��AD��6![]() ��AF��4
��AF��4![]() ����AE�ij���
����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ԥ��ij�����з�չǰ;����1600Ԫ����һ�����ϣ����к��Ȼ����Ӧ������6000Ԫ�����������ϣ��ڶ������ϵ������ǵ�һ����3���������۱ȵ�һ����2Ԫ.
(1)��һ�����Ͻ������۶���Ԫ��
(2)�����ι������ϰ�ͬһ�۸����ۣ�����ȫ���������������1200Ԫ����ô���۵�������Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com