
【题目】2022年北京冬奥会吉祥物“冰墩墩”以熊猫为原型进行设计创作,北京冬残奥会吉祥物“雪容融”则以中国标志性符号的灯笼为创意进行设计创作“冰墩墩”和“雪容融”是一个非常完美的搭:配和组合,是中国文化和奥林匹克精神又一次完美的结合莉莉有“冰墩墩”和“雪容融”的纪念邮票各2张(如图),这4张邮票背面完全相同,莉莉想给好友小婷和小华各送一张纪念邮票,她先让小婷从这4张邮票中随机抽取一张,然后,再让小华从剩下的3张中随机抽取一张.

(1)小婷抽到“冰墩墩”的纪念邮票的概率是__________.
(2)利用树状图或列表法求小婷和小华均抽到“雪容融”的纪念邮票的概率.
科目:初中数学 来源: 题型:
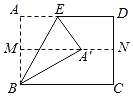
【题目】如图,对折矩形纸片ABCD使AD与BC重合,得到折痕MN,再把纸片展平.E是AD上一点,将△ABE沿BE折叠,使点A的对应点A′落在MN上.若CD=5,则BE的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
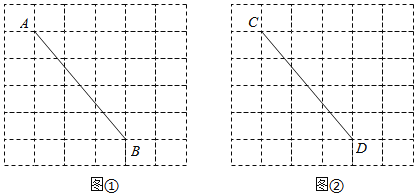
【题目】图①、图②均是6×6的正方形网格,每个小正方形的边长为1,小正方形的顶点称为格点,点A、B、C、D均在格点上.用直尺在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写画法.
(1)在图①中以线段AB为腰画一个等腰三角形ABM,画出的△ABM的面积是 .
(2)在图②中以线段CD为边画一个四边形CDEF,使∠FCD+∠EDC=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】茶叶是安徽省主要经济作物之一,2020年新茶上市期间,某茶厂为获得最大利益,根据市场行情,把新茶价格定为400元/kg,并根据历年的相关数据整理出第x天(1≤x≤15,且x为整数)制茶成本(含采摘和加工)和制茶量的相关信息如下表.假定该茶厂每天制作和销售的新茶没有损失,且能在当天全部售出(当天收入=日销售额-日制茶成本)
制茶成本(元/kg) | 150+10x |
制茶量(kg) | 40+4x |
(1)求出该茶厂第10天的收入;
(2)设该茶厂第x天的收入为y(元).试求出y与x之间的函数关系式,并求出y的最大值及此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
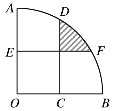
【题目】已知如图,扇形AOB的圆心角∠AOB=90°,OA=4,点C、点E分别是OB、OA的中点,CD⊥OB,EF⊥OA,则阴影部分面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
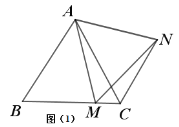
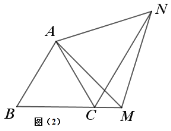
(1)如图(1),在等边三角形ABC中,点M是BC上的任意一点(不含端点B、C),连接AM,以AM为边作等边三角形AMN,连接CN,则∠ACN= °.
类比探究
(2)如图(2),在等边三角形ABC中,点M是BC延长线上的任意一点(不含端点C),其他条件不变,(1)中的结论还成立吗?请说明理由.
拓展延伸
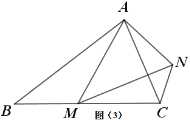
(3)如图(3),在等腰三角形ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连接AM,以AM为边作等腰三角形AMN,使AM=MN,连接CN.添加一个条件,使得∠ABC=∠ACN仍成立,写出你所添加的条件,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断中:①abc>0;②b2﹣4ac>0;③9a﹣3b+c=0;④若点(![]() ,y1),(﹣2,y2)均在抛物线上,则y1>y2;⑤5a﹣2b<0;其中正确的个数有( )
,y1),(﹣2,y2)均在抛物线上,则y1>y2;⑤5a﹣2b<0;其中正确的个数有( )
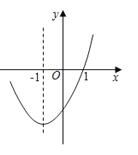
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
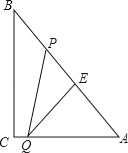
【题目】如图,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.点P从B出发沿BA向A运动,速度为每秒1cm,点E是点B以P为对称中心的对称点,点P运动的同时,点Q从A出发沿AC向C运动,速度为每秒2cm,当点Q到达顶点C时,P,Q同时停止运动,设P,Q两点运动时间为t秒.
(1)当t为何值时,PQ∥BC?
(2)设四边形PQCB的面积为y,求y关于t的函数关系式;
(3)四边形PQCB面积能否是△ABC面积的![]() ?若能,求出此时t的值;若不能,请说明理由;
?若能,求出此时t的值;若不能,请说明理由;
(4)当t为何值时,△AEQ为等腰三角形?(直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com