
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a、b满足(a﹣2)2+|b﹣4|=0,现同时将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=![]() S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP、∠DOP、∠APO之间满足的数量关系.
【答案】(1)8;(2)M(0,2)或(0,﹣2);(3)①∠APO=∠DOP+∠BAP;②∠DOP=∠BAP+∠APO;③∠BAP=∠DOP+∠APO.
【解析】
(1)先由非负数性质求出a=2,b=4,再根据平移规律,得出点C,D的坐标,然后根据四边形ABDC的面积=AB×OA即可求解;
(2)存在.设M坐标为(0,m),根据S△PAB=S四边形ABDC,列出方程求出m的值,即可确定M点坐标;
(3)分三种情况求解:①当点P在线段BD上移动时,②当点P在DB的延长线上时,③当点P在BD的延长线上时.
解:(1)∵(a﹣2)2+|b﹣4|=0,
∴a=2,b=4,
∴A(0,2),B(4,2).
∵将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,
∴C(﹣1,0),D(3,0).
∴S四边形ABDC=AB×OA=4×2=8;
(2)在y轴上存在一点M,使S△MCD=S四边形ABCD.设M坐标为(0,m).
∵S△MCD=![]() S四边形ABDC,
S四边形ABDC,
∴![]() ×4|m|=4,
×4|m|=4,
∴2|m|=4,
解得m=±2.
∴M(0,2)或(0,﹣2);
(3)①当点P在线段BD上移动时,∠APO=∠DOP+∠BAP
理由如下:
过点P作PE∥AB交OA于E.
∵CD由AB平移得到,则CD∥AB,
∴PE∥CD,
∴∠BAP=∠APE,∠DOP=∠OPE,
∴∠BAP+∠DOP=∠APE+∠OPE=∠APO,
②当点P在DB的延长线上时,同①的方法得,∠DOP=∠BAP+∠APO;
③当点P在BD的延长线上时,同①的方法得,∠BAP=∠DOP+∠APO.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0) 
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察图形:填空
(1)表示:1+3=4=22;
(2)表示:1+3+5=9=32;
(3)表示:1+3+5+7=16=42;
以此类推,(4)表示: ;
解决问题:求1+3+5+7+……+2019的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一组密码的一部分,请你运用所学知识找到破译的“钥匙”.目前,已破译出“正做数学”的真实意思是“祝你成功”.若“正”所处的位置为(x,y),你找到的密码钥匙是:横坐标_____,纵坐标_____,破译的“今天考试”真实意思是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若把边长为1的正方形ABCD的四个角(阴影部分)剪掉,得一四边形A1B1C1D1 . 试问怎样剪,才能使剩下的图形仍为正方形,且剩下图形的面积为原来正方形面积的 ![]() ,请说明理由.(写出证明及计算过程)
,请说明理由.(写出证明及计算过程) 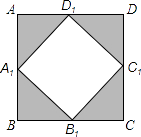
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运用运算律计算:
(1)0.36+(-7.4)+0.3+(-0.6)+0.64;
(2)(-103)+(+1![]() )+(-97)+(+100)+(-1
)+(-97)+(+100)+(-1![]() );
);
(3)(-3![]() )+(-2.16)+8
)+(-2.16)+8![]() +3
+3![]() +(-3.84)+(-0.25)+
+(-3.84)+(-0.25)+![]() ;
;
(4)(-![]() )+3
)+3![]() +|-0.75|+(-5
+|-0.75|+(-5![]() )+|-2
)+|-2![]() |.
|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤∠AGB+∠AED=145°.其中正确的个数是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若把边长为1的正方形ABCD的四个角(阴影部分)剪掉,得一四边形A1B1C1D1 . 试问怎样剪,才能使剩下的图形仍为正方形,且剩下图形的面积为原来正方形面积的 ![]() ,请说明理由.(写出证明及计算过程)
,请说明理由.(写出证明及计算过程) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE是∠AOC的平分线,∠BOC=130°,∠BOF=140°,则∠EOF的度数为( )

A. 95° B. 65°
C. 50° D. 40°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com