
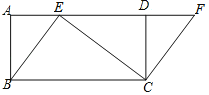
【题目】如图,四边形ABCD是矩形,点E在AD边上,点F在AD的延长线上,且BE=CF.
(1)求证:四边形EBCF是平行四边形.
(2)若∠BEC=90°,∠ABE=30°,AB=![]() ,求ED的长.
,求ED的长.
【答案】(1)证明见解析(2)3
【解析】试题分析:
(1)由AB=CD,BE=CF,可证Rt△BAE≌Rt△CDF,从而证得BE∥CF,即可得证;
(2)由题意可知∠2=30°,∠1=∠3=60°,在直角△ABE中求出AE,BE,在直角△BEC中求出BC的长,即可求出ED的长.
试题解析:
(1)证明:
∵四边形ABCD是矩形,∴∠A=∠CDF=∠ABC=90°,AB=DC,AD=BC,
在Rt△BAE和Rt△CDF中,
![]() ,
,
∴Rt△BAE≌Rt△CDF,∴∠1=∠F,∴BE∥CF,
又∵BE=CF,∴四边形EBCF是平行四边形.
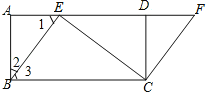
(2)解:∵Rt△BAE中,∠2=30°,AB=![]() ,
,
∴AE=ABtan∠2=1,![]() ,∠3=60°,
,∠3=60°,
在Rt△BEC中,![]() ,
,
∴AD=BC=4,
∴ED=AD﹣AE=4﹣1=3.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.

(1)填空:与∠AOE互补的角是 ;
(2)若∠AOD=36°,求∠DOE的度数;
(3)当∠AOD=x°时,请直接写出∠DOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:每购买500元商品,就能获得一次转动转盘的机会,如果转盘停止后,指针上对准500、20、100、50、10的区域,顾客就可以分别获得500元、200元、100元、50元、10元的购物券一张。(转盘等分成20份)

(1)小华购物450元,他获得购物券的概率是多少?
(2)小丽购物600元,那么她获得100元以上(包括100元)券的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题.
 程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
在《算法统宗》里记载了一道趣题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.试问大、小和尚各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,现有一张边长为4的正方形纸片![]() ,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米。
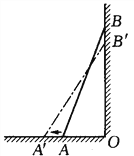
(1)这个梯子的顶端离地面有多高?
(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一外地游客到某特产专营店,准备购买精加工的豆腐乳和猕猴桃果汁两种盒装特产,若购买3盒豆腐乳和2盒猕猴桃果汁共需60元;购买1盒豆腐乳和3盒猕猴桃果汁共需55元.
(1)请分别求出每盒豆腐乳和每盒猕猴桃果汁的价格;
(2)该游客购买了4盒豆腐乳和2盒猕猴桃果汁,共需多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com