
【题目】如图所示,现有一张边长为4的正方形纸片![]() ,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;

【答案】(1)证明详见解析.(2)△PDH的周长不发生变化,理由详见解析
【解析】根据轴对称的性质以及角平分线上一点到角两边的距离相等即可解答.
试题分析:(1)∵四边形EBCF与四边形EPGF关于EF对称,∴∠BPH=∠PBC(轴对称性质)∵四边形ABCD为正方形,∴AD∥BC,∴∠APB=∠PBC,∴∠APB=∠BPH即得证.
(2) △PDH的周长不发生变化.由(1)知∠APB=∠BPH即BP为∠APH的角平分线,同理可得:BH为∠CHP的角平分线,过B作BM⊥PH于M,∵BP为∠APH的角平分线,∴PM=AP,∵BH为∠CHP的角平分线,∴MH=CH,∴PH=PM+MH=AP+CH,∴△PDH的周长为DP+PH+DH= DP+AP+CH+DH=AD+CD=8
∴当点P在边AD上移动时,△PDH的周长不发生变化.


科目:初中数学 来源: 题型:
【题目】如图①,已知二次函数y=﹣x2+2x+3的图象与x轴交于点A,B,与y轴交于点C.
(1)求△ABC的面积.
(2)点M在OB边上以每秒1个单位的速度从点O向点B运动,点N在BC边上以每秒 ![]() 个单位得速度从点B向点C运动,两个点同时开始运动,同时停止.设运动的时间为t秒,试求当t为何值时,以B,M,N为顶点的三角形与△BOC相似?
个单位得速度从点B向点C运动,两个点同时开始运动,同时停止.设运动的时间为t秒,试求当t为何值时,以B,M,N为顶点的三角形与△BOC相似?
(3)如图②,点P为抛物线上的动点,点Q为对称轴上的动点,是否存在点P,Q,使得以P,Q,C,B为顶点的四边形是平行四变形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE∥BD,过点D作ED∥AC,两线相交于点E. 
(1)求证:四边形AODE是菱形;
(2)连接BE,交AC于点F.若BE⊥ED于点E,求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在AD边上,点F在AD的延长线上,且BE=CF.
(1)求证:四边形EBCF是平行四边形.
(2)若∠BEC=90°,∠ABE=30°,AB=![]() ,求ED的长.
,求ED的长.
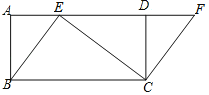
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代对勾股定理有深刻的认识.
(1)三国时代吴国数学家赵爽第一次对勾股定理加以证明:用四个全等的图1所示的直角三角形拼成一个图2所示的大正方形,中间空白部分是一个小正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边分别为a,b,求(a+b)2的值;
(2)清朝的康熙皇帝对勾股定理也很有研究,他著有《积求勾股法》:用现代的数学语言描述就是:若直角三角形的三边长分别为3,4,5的整数倍,设其面积为S,则求其边长的方法为:第一步![]() =m;第二步:
=m;第二步: ![]() =k;第三步:分别用3,4,5乘k,得三边长.当面积S等于150时,请用“积求勾股法”求出这个直角三角形的三边长.
=k;第三步:分别用3,4,5乘k,得三边长.当面积S等于150时,请用“积求勾股法”求出这个直角三角形的三边长.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com