
【题目】解方程:
(1)2x+3=x+5;
(2)2(3y-1)-3(2-4y)=9y+10;
(3)![]()
(4)![]() .
.
【答案】(1)x=2(2)y=2(3)x=3(4)y=-1
【解析】
(1)移项、合并同类项即可得解;
(2)去括号、移项、合并同类项、系数化为1即可得解;
(3)去括号、去分母、移项、合并同类项、系数化为1即可得解;
(4)去分母、去括号、移项、合并同类项、系数化为1即可得解;
(1)移项,得2x-x=5-3,
合并同类项,得x=2;
(2)去括号,得6y-2-6+12y=9y+10,
移项,得6y+12y-9y=10+2+6,
合并同类项,得9y=18,
系数化为1,得y=2;
(3)去括号,得![]() x+
x+![]() x+2=8+x,
x+2=8+x,
去分母,得x+5x+4=16+2x,
移项,得x+5x-2x=16-4,
合并同类项,得4x=12,
系数化为1,得x=3;
(4)去分母,得3(3y-1)-12=2(5y-7),
去括号,得9y-3-12=10y-14,
移项,得9y-10y=3+12-14,
合并同类项,得-y=1,
系数化为1,得y=-1.


科目:初中数学 来源: 题型:
【题目】如图①、②、③、④四个图形都是平面图形,观察图②和表中对应数值,探究计数的方法并解答下面的问题.

(1)数一数每个图各有多少顶点、多少条边、这些边围成多少区域,将结果填入下表:
图形 | ① | ② | ③ | ④ |
顶点数(V) | ||||
边数(E) | ||||
区域数(F) |
(2)根据表中的数值,写出平面图的顶点数、边数、区域数之间的关系;
(3)如果一个平面图形有20个顶点和11个区域,求这个平面图形的边数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,现有一张边长为4的正方形纸片![]() ,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列三个判断中:
①当x>0时,y>0;
②若a=﹣1,则b=4;
③抛物线上有两点P(x1 , y1)和Q(x2 , y2),若x1<1<x2 , 且x1+x2>2,则y1>y2;正确的是( )
A.①
B.②
C.③
D.①②③都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米。
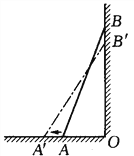
(1)这个梯子的顶端离地面有多高?
(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.
(1)当点C,E,F在直线AB的同侧时(如图①所示),试说明∠BOE=2∠COF.
(2)当点C与点E,F在直线AB的两侧时(如图②所示),(1)中的结论是否仍然成立?请给出你的结论,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D,那么∠DAC的度数为( )

A. 90° B. 80° C. 70° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为( )

A. 40° B. 45° C. 60° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程2(x﹣3)﹣m=2的解和方程3x﹣7=2x的解相同.
(1)求m的值;
(2)已知线段AB=m,在直线AB上取一点P,恰好使AP=2PB,点Q为PB的中点,求线段AQ的长.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com