
【题目】如图①、②、③、④四个图形都是平面图形,观察图②和表中对应数值,探究计数的方法并解答下面的问题.

(1)数一数每个图各有多少顶点、多少条边、这些边围成多少区域,将结果填入下表:
图形 | ① | ② | ③ | ④ |
顶点数(V) | ||||
边数(E) | ||||
区域数(F) |
(2)根据表中的数值,写出平面图的顶点数、边数、区域数之间的关系;
(3)如果一个平面图形有20个顶点和11个区域,求这个平面图形的边数.
【答案】(1)见表格解析;(2)V+F=E+1;(3)30.
【解析】
(1)根据图中的四个平面图形数出其顶点数、边数、区域数得出结果;
(2)根据表(1)数据总结出归律;
(3)根据题(2)的公式把20个顶点和11个区域代入即可得平面图形的边数.
(1)结和图形我们可以得出:
图①有4个顶点、6条边、这些边围成3个区域;
图②有7个顶点、9条边、这些边围成3个区域;
图③有8个顶点、12条边、这些边围成5个区域;
图④有10个顶点、15条边、这些边围成6区域.
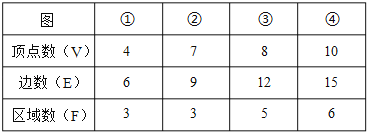
(2)根据以上数据,顶点用V表示,边数用E表示,区域用F表示,他们的关系可表示为:V+F=E+1;
(3)把V=20,F=11代入上式得:E=V+F﹣1=20+11﹣1=30.故如果平面图形有20个顶点和11个区域,那么这个平面图形的边数为30.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图是两个可以自由转动的转盘,转盘A被分成三个面积相等的扇形,转盘B被分成两个面积相等的扇形. 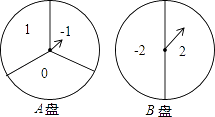
(1)转动转盘A一次,所得到的数字是负数的概率为
(2)转动两个转盘各一次,请用列表法或画树状图法求所得到的数字均是负数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知二次函数y=﹣x2+2x+3的图象与x轴交于点A,B,与y轴交于点C.
(1)求△ABC的面积.
(2)点M在OB边上以每秒1个单位的速度从点O向点B运动,点N在BC边上以每秒 ![]() 个单位得速度从点B向点C运动,两个点同时开始运动,同时停止.设运动的时间为t秒,试求当t为何值时,以B,M,N为顶点的三角形与△BOC相似?
个单位得速度从点B向点C运动,两个点同时开始运动,同时停止.设运动的时间为t秒,试求当t为何值时,以B,M,N为顶点的三角形与△BOC相似?
(3)如图②,点P为抛物线上的动点,点Q为对称轴上的动点,是否存在点P,Q,使得以P,Q,C,B为顶点的四边形是平行四变形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠BAC=90°,AB=AC,点D在边BC上,以AD为边作正方形ADEF,连结CF,CE.
(1)求证:△ABD≌△ACF;
(2)如果BD=AC,求证:CD=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了应对金融危机,节俭开支,我区某康庄工程指挥部,要对某路段建设工程进行招标,从甲、乙两个工程队的投标书中得知:每天需支付甲队的工程款1.5万元,乙队的工程款1.1万元.甲、乙两个工程队实际施工方案如下:
(1)甲队单独完成这项工程刚好能够如期完成;
(2)乙队单独完成这项工程要比规定的时间多用10天;
(3)若甲、乙两队合作8天,余下的由乙队单独做也正好如期完成.
试问:在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE∥BD,过点D作ED∥AC,两线相交于点E. 
(1)求证:四边形AODE是菱形;
(2)连接BE,交AC于点F.若BE⊥ED于点E,求∠AOD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com