
【题目】为了应对金融危机,节俭开支,我区某康庄工程指挥部,要对某路段建设工程进行招标,从甲、乙两个工程队的投标书中得知:每天需支付甲队的工程款1.5万元,乙队的工程款1.1万元.甲、乙两个工程队实际施工方案如下:
(1)甲队单独完成这项工程刚好能够如期完成;
(2)乙队单独完成这项工程要比规定的时间多用10天;
(3)若甲、乙两队合作8天,余下的由乙队单独做也正好如期完成.
试问:在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
【答案】应选择方案(3)施工方案能节省工程款,理由见解析
【解析】试题分析:应先求出甲乙两人的工效.等量关系:甲做8天的工作量+乙做规定时间的工作量=1.在保证工期的前提下,算出各个方案所需费用进行比较即可.
试题解析:设甲队单独完成需x天,则乙队单独完成需(x+10)天,
依题意得
![]() ,
,
解得x=40,
经检验:x=40是原方程的根,
∴x+10=40+10=50,
∴方案(1)的工程款=40×1.5=60(万元),
方案(2)不合题意,舍去,
方案(3)的工程款=8×1.5+40×1.1=56(万元),
∵60>56∴在不耽误工期的前提下,应选择方案(3)施工方案能节省工程款,
答:应选择方案(3)施工方案能节省工程款.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知直线l:y=﹣x+2与x轴交于点A、与y轴交于点B.抛物线y=ax2+bx+c(a≠0)经过O、A两点,与直线l交于点C,点C的横坐标为﹣1.
(1)求该抛物线的函数表达式;
(2)若点P是位于直线l下方抛物线上的一个动点,且不与点A、点C重合,连接PA、PC.设△PAC的面积为S,求当S取得最大值时点P的坐标,并求S的最大值;
(3)如图2,设抛物线的顶点为D,连接AD、BD.点E是对称轴m上一点,F是抛物线上一点,请直接写出当△DEF与△ABD相似时点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D,E,F分别在三边上,且BE=CD,BD=CF,G为EF的中点.
(1)若∠A=40°,求∠B的度数;
(2)试说明:DG垂直平分EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠BOD= ______ °时,四边形BECD是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①、②、③、④四个图形都是平面图形,观察图②和表中对应数值,探究计数的方法并解答下面的问题.

(1)数一数每个图各有多少顶点、多少条边、这些边围成多少区域,将结果填入下表:
图形 | ① | ② | ③ | ④ |
顶点数(V) | ||||
边数(E) | ||||
区域数(F) |
(2)根据表中的数值,写出平面图的顶点数、边数、区域数之间的关系;
(3)如果一个平面图形有20个顶点和11个区域,求这个平面图形的边数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点分别为A(2,3),B(3,1),C(-2,-2).
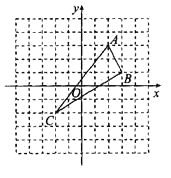
(1)请在图中作出△ABC关于y轴的轴对称图形△A′B′C′(A,B,C的对称点分别是A′,B′,C′),并直接写出A′,B′,C′的坐标.
(2)求△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB//DE,AC//DF,AC=DF,下列条件中不能判断△ABC≌△DEF的是( )

A. AB=DE B. EF=BC C. ∠B=∠E D. EF∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,平行四边形
,平行四边形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() .将直线
.将直线![]() 绕点
绕点![]() 顺时针旋转分别交
顺时针旋转分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.

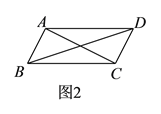
(![]() )在旋转过程中,线段
)在旋转过程中,线段![]() 与
与![]() 的数量关系是__________.
的数量关系是__________.
(![]() )如图
)如图![]() ,若
,若![]() ,当旋转角至少为__________
,当旋转角至少为__________![]() 时,四边形
时,四边形![]() 是平行四边形,并证明此时的四边形是
是平行四边形,并证明此时的四边形是![]() 是平行四边形.
是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.
(1)当点C,E,F在直线AB的同侧时(如图①所示),试说明∠BOE=2∠COF.
(2)当点C与点E,F在直线AB的两侧时(如图②所示),(1)中的结论是否仍然成立?请给出你的结论,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com