
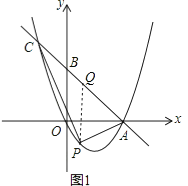
【题目】如图1,已知直线l:y=﹣x+2与x轴交于点A、与y轴交于点B.抛物线y=ax2+bx+c(a≠0)经过O、A两点,与直线l交于点C,点C的横坐标为﹣1.
(1)求该抛物线的函数表达式;
(2)若点P是位于直线l下方抛物线上的一个动点,且不与点A、点C重合,连接PA、PC.设△PAC的面积为S,求当S取得最大值时点P的坐标,并求S的最大值;
(3)如图2,设抛物线的顶点为D,连接AD、BD.点E是对称轴m上一点,F是抛物线上一点,请直接写出当△DEF与△ABD相似时点E的坐标.
【答案】
(1)
解:当x=﹣1时,y=﹣x+2=3,则C(﹣1,3),
当y=0时,﹣x+2=0,解得x=2,则A(2,0),
∵抛物线过点O(0,0)、A(2,0),
设抛物线解析式为y=ax( x﹣2 ),
将点C(﹣1,3)代入得3=﹣a(﹣1﹣2 ),解得a=1,
∴该抛物线解析式为y=x( x﹣2 ),即y=x2﹣2x
(2)
解:设P(m,m2﹣2m),过点P作PQ∥y轴,交直线l于点Q,如图1,则Q(m,﹣m+2),
∴PQ=(﹣m+2 )﹣(m2﹣2m)=﹣m2+m+2,
∴S=S△PQC+S△PQA= ![]() (2+1)PQ=﹣
(2+1)PQ=﹣ ![]() m2+
m2+ ![]() m+3=﹣
m+3=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() ,
,
∴当m= ![]() 时,S有最大值,最大值为
时,S有最大值,最大值为 ![]() ,
,
把m= ![]() 代入m2﹣2m得m2﹣2m=﹣
代入m2﹣2m得m2﹣2m=﹣ ![]() ,
,
∴P( ![]() ,﹣
,﹣ ![]() )
)
(3)
解:设F点坐标为(t,t2﹣2t),
当x=1时,y=x2﹣2x=﹣1,则D(1,﹣1),当x=0时,y=﹣x+2=2,则B(0,2),
∵AB2=22+22=8,AD2=12+12=2,DB2=12+(2+1)2=10,
∴AB2+AD2=DB2,
∴△ABD为直角三角形,∠BAD=90°,
如图2,
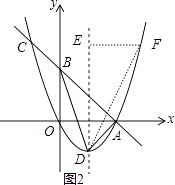
当△DEF∽△BAD,则∠DEF=∠BAD=90°, ![]() =
= ![]() ,即DE:2
,即DE:2 ![]() =EF:
=EF: ![]() ,
,
∴DE=2EF,
∵EF⊥DE,
∴E(1,t2﹣2t),
∴t2﹣2t+1=2(t﹣1),解得t1=1(舍去),t2=3,此时E点坐标为(1,3);
当△DEF∽△DAB,则∠DEF=∠BAD=90°, ![]() =
= ![]() ,即DE:
,即DE: ![]() =EF:2
=EF:2 ![]() ,
,
∴DE= ![]() EF,
EF,
∵EF⊥DE,
∴E(1,t2﹣2t),
∴t2﹣2t+1= ![]() (t﹣1),解得t1=1(舍去),t2=
(t﹣1),解得t1=1(舍去),t2= ![]() ,此时E点坐标为(1,﹣
,此时E点坐标为(1,﹣ ![]() );
);
如图3,
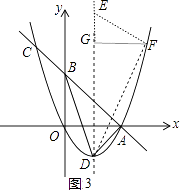
当△DFE∽△BAD,则∠DFE=∠BAD=90°,∠FDE=∠ADB,
过F点作FG⊥DE于G,则△DGF∽△BAD,同样方法可得G(1,3),则F(3,3),
∵GF2=GEGD,即22=GE4,
∴GE=1,
∴此时E点坐标为(1,4);
当△DFE∽△DAB,则∠DFE=∠BAD=90°,用同样方法可得E点坐标为(1, ![]() ),
),
综上所述,E点坐标为(1,3),(1,4),(1, ![]() ),(1,﹣
),(1,﹣ ![]() ).
).
【解析】(1)先根据一次函数图象上点的坐标特征求出C(﹣1,3),A(2,0),再设交点式y=ax( x﹣2 ),然后把点C点坐标代入求出a即可得到该抛物线解析式为y=x2﹣2x;(2)设P(m,m2﹣2m),过点P作PQ∥y轴,交直线l于点Q,如图1,则Q(m,﹣m+2),则PQ=﹣m2+m+2,根据三角形面积公式,利用S=S△PQC+S△PQA可得到S=﹣ ![]() m2+
m2+ ![]() m+3,然后根据二次函数的性质解决最值问题(3)设F点坐标为(t,t2﹣2t),先确定D(1,﹣1),B(0,2),再利用勾股定理的逆定理证明△ABD为直角三角形,∠BAD=90°,然后分类讨论:如图2,当△DEF∽△BAD,则∠DEF=∠BAD=90°,利用相似比得DE=2EF,由于EF⊥DE,则E(1,t2﹣2t),所以t2﹣2t+1=2(t﹣1),解得t1=1(舍去),t2=3,易得此时E点坐标为(1,3);当△DEF∽△DAB,则∠DEF=∠BAD=90°,
m+3,然后根据二次函数的性质解决最值问题(3)设F点坐标为(t,t2﹣2t),先确定D(1,﹣1),B(0,2),再利用勾股定理的逆定理证明△ABD为直角三角形,∠BAD=90°,然后分类讨论:如图2,当△DEF∽△BAD,则∠DEF=∠BAD=90°,利用相似比得DE=2EF,由于EF⊥DE,则E(1,t2﹣2t),所以t2﹣2t+1=2(t﹣1),解得t1=1(舍去),t2=3,易得此时E点坐标为(1,3);当△DEF∽△DAB,则∠DEF=∠BAD=90°, ![]() =
= ![]() ,利用相似比得DE=
,利用相似比得DE= ![]() EF,
EF,
由EF⊥DE得到E(1,t2﹣2t),则t2﹣2t+1= ![]() (t﹣1),解得t1=1(舍去),t2=
(t﹣1),解得t1=1(舍去),t2= ![]() ,易得此时E点坐标为(1,﹣
,易得此时E点坐标为(1,﹣ ![]() );如图3,当△DFE∽△BAD,则∠DFE=∠BAD=90°,∠FDE=∠ADB,过F点作FG⊥DE于G,则△DGF∽△BAD,用前面方法可得G(1,3),则F(3,3),利用GF2=GEGD可计算出GE=1,则此时E点坐标为(1,4);当△DFE∽△DAB,则∠DFE=∠BAD=90°,用同样方法可得E点坐标为(1,
);如图3,当△DFE∽△BAD,则∠DFE=∠BAD=90°,∠FDE=∠ADB,过F点作FG⊥DE于G,则△DGF∽△BAD,用前面方法可得G(1,3),则F(3,3),利用GF2=GEGD可计算出GE=1,则此时E点坐标为(1,4);当△DFE∽△DAB,则∠DFE=∠BAD=90°,用同样方法可得E点坐标为(1, ![]() ).
).
【考点精析】根据题目的已知条件,利用一次函数的性质和二次函数的图象的相关知识可以得到问题的答案,需要掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.


科目:初中数学 来源: 题型:
【题目】已知关于x的方程(1﹣2k)x2﹣2![]() x﹣1=0
x﹣1=0
(1)若此方程为一元一次方程,求k的值.
(2)若此方程为一元二次方程,且有实数根,试求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内,△ABC和△ABD如图①放置,其中AB=BD.
小明做了如下操作:
将△ABC绕着边AC的中点旋转180°得到△CEA,将△ABD绕着边AD的中点旋转180°得到△DFA,如图②,请完成下列问题:
(1)试猜想四边形ABDF是什么特殊四边形,并说明理由;
(2)连接EF,CD,如图③,求证:四边形CDEF是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数图象经过点(-1,2).
(1)求此正比例函数的表达式;
(2)画出这个函数图象;
(3)点(2,-5)是否在此函数图象上?
(4)若这个图象还经过点A(a,8),求点A的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是两个可以自由转动的转盘,转盘A被分成三个面积相等的扇形,转盘B被分成两个面积相等的扇形. 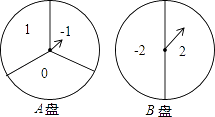
(1)转动转盘A一次,所得到的数字是负数的概率为
(2)转动两个转盘各一次,请用列表法或画树状图法求所得到的数字均是负数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
①abc<0;②b2﹣4ac>0;③3a+c<0;④16a+4b+c>0.
其中正确结论的个数是( )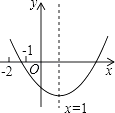
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张背面相同的纸牌A,B,C,D,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀后放在桌面上. 
(1)小红从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明从这四张纸牌中随机摸出两张,用树状图或表格法,求摸出的两张牌面图形都是中心对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,Rt△ABC中,∠ABC=90°,BC<AB<2BC.在AB边上取一点M,使AM=BC,过点A作AE⊥AB且AE=BM,连接EC,再过点A作AN∥EC,交直线CM、CB于点F、N.
(1)证明:∠AFM=45°;
(2)若将题中的条件“BC<AB<2BC”改为“AB>2BC”,其他条件不变,请你在图2的位置上画出图形,(1)中的结论是否仍然成立?如果成立,请说明理由;如果不成立,请猜想∠AFM的度数,并说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了应对金融危机,节俭开支,我区某康庄工程指挥部,要对某路段建设工程进行招标,从甲、乙两个工程队的投标书中得知:每天需支付甲队的工程款1.5万元,乙队的工程款1.1万元.甲、乙两个工程队实际施工方案如下:
(1)甲队单独完成这项工程刚好能够如期完成;
(2)乙队单独完成这项工程要比规定的时间多用10天;
(3)若甲、乙两队合作8天,余下的由乙队单独做也正好如期完成.
试问:在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com