
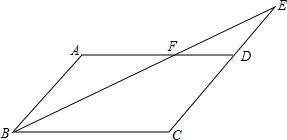
 如图,在?ABCD中,E是CD的延长线上一点,BE与AD交于点F,AF=DE=3,BC=5,求AB的长.
如图,在?ABCD中,E是CD的延长线上一点,BE与AD交于点F,AF=DE=3,BC=5,求AB的长. 分析 由在?ABCD中,AF=DE=3,BC=5,根据平行四边形的对边平行且相等,可求得AD的长,继而求得DF的长,易证得△ABF∽△DEF,然后由相似三角形的对应边成比例,求得答案.
解答 解:∵四边形ABCD是平行四边形,
∴AD=BC=5,AB∥CD,
∴△ABF∽△DEF,DF=AD-AF=5-3=2,
∴$\frac{AB}{DE}=\frac{AF}{DF}$,
∵AF=DE=3,
∴$\frac{AB}{3}=\frac{3}{2}$,
解得:AB=4.5.
点评 此题考查了平行四边形的性质以及相似三角形的判定与性质.注意平行四边形的对边相等且相等,相似三角形的对应边成比例.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
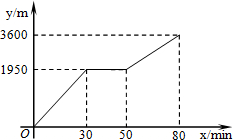 “五一”黄金周期间,甲乙两人相约去宾县二龙山游玩,两人到山脚下缆车起点,甲乙准备上山顶游玩,甲乘坐缆车,乙步行,两人相约在山顶的缆车终点会合,已知乙从山脚下缆车起点走到山顶缆车终点的路程是缆车从山脚下缆车起点到山顶缆车终点的线路长的2倍.由于乘坐缆车的人比较多,甲在乙出发后50min才乘上缆车,缆车的平均速度为180m/min,设乙出发x min后行走的路程为y m,图中的折线表示乙在整个过程中y与x的函数关系,下列问题叙述正确的个数有( )
“五一”黄金周期间,甲乙两人相约去宾县二龙山游玩,两人到山脚下缆车起点,甲乙准备上山顶游玩,甲乘坐缆车,乙步行,两人相约在山顶的缆车终点会合,已知乙从山脚下缆车起点走到山顶缆车终点的路程是缆车从山脚下缆车起点到山顶缆车终点的线路长的2倍.由于乘坐缆车的人比较多,甲在乙出发后50min才乘上缆车,缆车的平均速度为180m/min,设乙出发x min后行走的路程为y m,图中的折线表示乙在整个过程中y与x的函数关系,下列问题叙述正确的个数有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
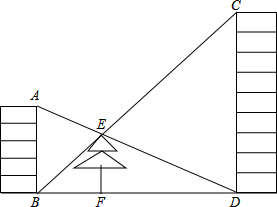 如图,在高5m的房顶A处望一楼的底部D,视线刚好过小树的顶端E,又从楼顶C处望房顶部B,视线也正好过小树的顶端E,测得小树高4m,求楼高CD.
如图,在高5m的房顶A处望一楼的底部D,视线刚好过小树的顶端E,又从楼顶C处望房顶部B,视线也正好过小树的顶端E,测得小树高4m,求楼高CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
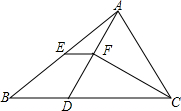 如图,在△ABC中,D在BC上,且CD=CA,CF平分∠ACB,AE=EB
如图,在△ABC中,D在BC上,且CD=CA,CF平分∠ACB,AE=EB查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | ab<1 | C. | $\frac{a}{b}$<1 | D. | $\frac{a}{b}$>1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com