
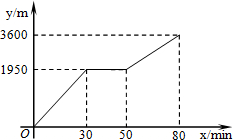
 “五一”黄金周期间,甲乙两人相约去宾县二龙山游玩,两人到山脚下缆车起点,甲乙准备上山顶游玩,甲乘坐缆车,乙步行,两人相约在山顶的缆车终点会合,已知乙从山脚下缆车起点走到山顶缆车终点的路程是缆车从山脚下缆车起点到山顶缆车终点的线路长的2倍.由于乘坐缆车的人比较多,甲在乙出发后50min才乘上缆车,缆车的平均速度为180m/min,设乙出发x min后行走的路程为y m,图中的折线表示乙在整个过程中y与x的函数关系,下列问题叙述正确的个数有( )
“五一”黄金周期间,甲乙两人相约去宾县二龙山游玩,两人到山脚下缆车起点,甲乙准备上山顶游玩,甲乘坐缆车,乙步行,两人相约在山顶的缆车终点会合,已知乙从山脚下缆车起点走到山顶缆车终点的路程是缆车从山脚下缆车起点到山顶缆车终点的线路长的2倍.由于乘坐缆车的人比较多,甲在乙出发后50min才乘上缆车,缆车的平均速度为180m/min,设乙出发x min后行走的路程为y m,图中的折线表示乙在整个过程中y与x的函数关系,下列问题叙述正确的个数有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 ①②通过运用函数图象的分析可以求出乙行走的总路程及途中休息的时间;
③直接运用待定系数法就可以求出解析式;
④运用乙行驶的全程求出甲行驶的路程,就可以求出甲行驶完全程用的时间,再代入其解析式就可以求出结论.
解答 解:由图象得:乙行走的总路程是:3600米,他途中休息了20分钟.
故①②正确;
当50≤x≤80时,设y与x的函数关系式为y=kx+b.根据题意得:
$\left\{\begin{array}{l}{1950=50k+b}\\{3600=80k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=55}\\{b=-800}\end{array}\right.$,
∴y与x的函数关系式为:y=55x-800,故③正确;
④缆车到山顶的路线长为3600÷2=1800(m),
缆车到达终点所需时间为1800÷180=10(min).
甲到达缆车终点时,乙行走的时间为10+50=60(min).
把x=60代入y=55x-800,得y=55×60-800=2500.
所以,当甲到达缆车终点时,
乙离缆车终点的路程是:3600-2500=1100(m),故④正确;
故选A.
点评 本题是一道有关行程问题的一次函数综合试题,考查了待定系数法求函数的解析式的运用,一次函数图象的性质的运用,在解答时读懂图象是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
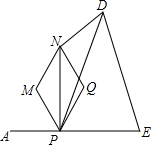 如图,已知线段AE=10,点P是线段AE上的动点,以AP长为边长作菱形PMNQ,已知该菱形的一个锐角∠MPQ=60°,且对角线NP⊥AE,△PED是以PE为底的等腰三角形,则△PND的面积的最大值是$\frac{25\sqrt{3}}{4}$.
如图,已知线段AE=10,点P是线段AE上的动点,以AP长为边长作菱形PMNQ,已知该菱形的一个锐角∠MPQ=60°,且对角线NP⊥AE,△PED是以PE为底的等腰三角形,则△PND的面积的最大值是$\frac{25\sqrt{3}}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
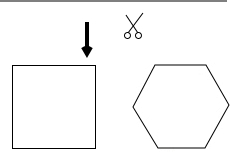 如图,用一根40cm长的铁丝剪成两段,分别做成边长均为整数的正方形和正六边形,则剪成的正方形和正六边形的边长相等的概率是$\frac{1}{3}$.
如图,用一根40cm长的铁丝剪成两段,分别做成边长均为整数的正方形和正六边形,则剪成的正方形和正六边形的边长相等的概率是$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
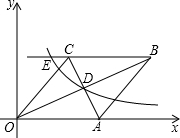 如图:已知,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=$\frac{k}{x}$(x>0),经过D点,交BC的延长线于E点,E点的坐标是(5,8).
如图:已知,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=$\frac{k}{x}$(x>0),经过D点,交BC的延长线于E点,E点的坐标是(5,8).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com