
分析 二次函数y=mx2-(1-m)x+m的图象和x轴无交点时,△<0,即(1-m)2-4m2<0,再加上m≠0即可.
解答 解:∵二次函数y=mx2-(1-m)x+m的图象和x轴无交点,
∴m≠0,△<0,
即(1-m)2-4m2<0,
整理得:-3m2-2m+1<0,
若-3m2-2m+1=0时,解得:m1=-1,m2=$\frac{1}{3}$,
∴-3m2-2m+1<0的解集为:m<-1或m>$\frac{1}{3}$.
∴m<-1或m>$\frac{1}{3}$时,二次函数y=mx2-(1-m)x+m与x轴无交点.
点评 该题考查函数图象与坐标轴的交点判断,当△=b2-4ac>0时图象与x轴有两个交点;当△=b2-4ac=0时图象与x轴有一个交点;当△=b2-4ac<0时图象与x轴没有交点.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
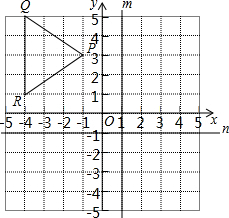 已知:△PQR在平面直角坐标系中的位置如图所示:
已知:△PQR在平面直角坐标系中的位置如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
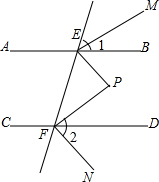 如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P.∠1与∠2的平分线EM,FN,判断EM,FN所在的直线有什么位置关系,并说明理由.
如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P.∠1与∠2的平分线EM,FN,判断EM,FN所在的直线有什么位置关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
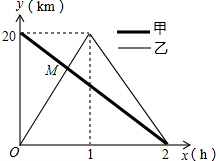 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象,根据图象解答以下问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
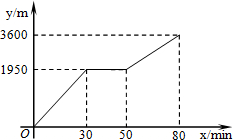 “五一”黄金周期间,甲乙两人相约去宾县二龙山游玩,两人到山脚下缆车起点,甲乙准备上山顶游玩,甲乘坐缆车,乙步行,两人相约在山顶的缆车终点会合,已知乙从山脚下缆车起点走到山顶缆车终点的路程是缆车从山脚下缆车起点到山顶缆车终点的线路长的2倍.由于乘坐缆车的人比较多,甲在乙出发后50min才乘上缆车,缆车的平均速度为180m/min,设乙出发x min后行走的路程为y m,图中的折线表示乙在整个过程中y与x的函数关系,下列问题叙述正确的个数有( )
“五一”黄金周期间,甲乙两人相约去宾县二龙山游玩,两人到山脚下缆车起点,甲乙准备上山顶游玩,甲乘坐缆车,乙步行,两人相约在山顶的缆车终点会合,已知乙从山脚下缆车起点走到山顶缆车终点的路程是缆车从山脚下缆车起点到山顶缆车终点的线路长的2倍.由于乘坐缆车的人比较多,甲在乙出发后50min才乘上缆车,缆车的平均速度为180m/min,设乙出发x min后行走的路程为y m,图中的折线表示乙在整个过程中y与x的函数关系,下列问题叙述正确的个数有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com