Question

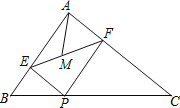
【题目】如图，在Rt△ABC中，∠BAC=90°，AB=6，AC=8，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值是 ．

Answer 1

【答案】

【解析】

试题分析：根据矩形的性质就可以得出EF，AP互相平分，且EF=AP，根据垂线段最短的性质就可以得出AP⊥BC时，AP的值最小，即AM的值最小，由勾股定理求出BC，根据面积关系建立等式求出其解即可．

解：∵PE⊥AB，PF⊥AC，∠BAC=90°，

∴∠EAF=∠AEP=∠AFP=90°，

∴四边形AEPF是矩形，

∴EF，AP互相平分．且EF=AP，

∴EF，AP的交点就是M点，

∵当AP的值最小时，AM的值就最小，

∴当AP⊥BC时，AP的值最小，即AM的值最小．

∵AP×BC=AB×AC，

∴AP×BC=AB×AC，

在Rt△ABC中，由勾股定理，得BC==10，

∵AB=6，AC=8，

∴10AP=6×8，

∴AP=

∴AM=，

故答案为：．