
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),B两点,与y轴交于点C(0,3),抛物线的顶点在直线x=1上.
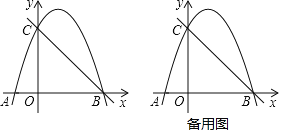
(1)求抛物线的解析式;
(2)点P为第一象限内抛物线上的一个动点,过点P做PQ∥y轴交BC与点Q,当点P在何位置时,线段PQ的长度有最大值?
(3)点M在x轴上,点N在抛物线对称轴上,是否存在点M,点N,使以点M,N,C,B为顶点的四边形是平行四边形?若存在,请求出点M的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2+2x+3;(2)点P的坐标为(![]() ,
,![]() );(3)存在,点M的坐标为(4,0)或(﹣2,0)或(2,0)
);(3)存在,点M的坐标为(4,0)或(﹣2,0)或(2,0)
【解析】
(1)点A(﹣1,0),点C(0,3),顶点在直线x=1上,则c=3,点B(3,0),故抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),即可求解;
(2)设点P(t,﹣t2+2t+3),Q(t,﹣t+3).则PQ=﹣t2+3t,即可求解;
(3)分BC是平行四边形的边、BC是平行四边形的对角线两种情况,分别求解即可.
(1)∵抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),B两点,顶点在直线x=1上,
∴点B(3,0),
∵抛物线与y轴交于点C(0,3),
∴c=3,
设抛物线的表达式为:y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),
∴﹣3a=3,解得:a=﹣1,
∴抛物线的表达式为:y=﹣x2+2x+3;
(2)设直线BC的解析式为y=kx+b,
将点B、C的坐标代入得: ![]() ,
,
解得![]() ,
,
直线BC的解析式为y=﹣x+3,
设点P(t,﹣t2+2t+3),则Q(t,﹣t+3).
∴PQ=﹣t2+3t=![]() ,
,
∴当t=![]() 时,PQ长度的最大值为
时,PQ长度的最大值为![]() ,
,
此时﹣t2+2t+3=![]() ,
,
∴点P的坐标为(![]() ,
,![]() );
);
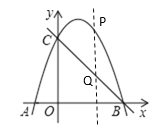
(3)设点M(m,0)、点N(1,n),点C(0,3)、点B(3,0),
①当BC是平行四边形的边时,
点C向右平移3个单位向下平移3个单位得到B,
同理点C(B)向右平移3个单位向下平移3个单位得到B(C),
即1+3=m或1﹣3=m,解得:m=4或﹣2;
②当BC是平行四边形的对角线时,
由中点公式得:1+m=3,解得:m=2,
故点M的坐标为(4,0)或(﹣2,0)或(2,0).


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
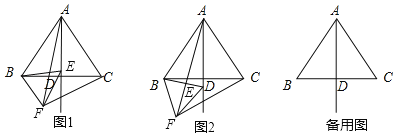
【题目】已知△ABC是等边三角形,AD⊥BC于点D,点E是直线AD上的动点,将BE绕点B顺时针方向旋转60°得到BF,连接EF、CF、AF.
(1)如图1,当点E在线段AD上时,猜想∠AFC和∠FAC的数量关系;(直接写出结果)
(2)如图2,当点E在线段AD的延长线上时,(1)中的结论还成立吗?若成立,请证明你的结论,若不成立,请写出你的结论,并证明你的结论;
(3)点E在直线AD上运动,当△ACF是等腰直角三角形时,请直接写出∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果按此速度增涨,该公司六月份的快递件数将达到多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
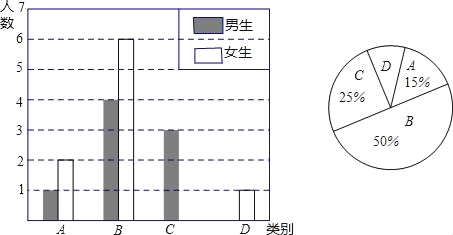
【题目】李老师为了了解班级学生自主学习、合作交流的具体情况,对九(1)班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C;一般;D:较差,并将调查结果绘制成以下两幅不完整的统计图.请你根据统计图解答下列问题:
(1)本次调查中,李老师一共调查了 名同学,其中女生共有 名.
(2)将上面的条形统计图补充完整;
(3)为了共同进步,李老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请求所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
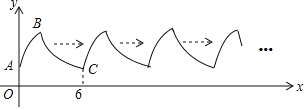
【题目】如图,曲线AB是顶点为B,与y轴交于点A的抛物线y=﹣x2+4x+2的一部分;曲线BC是双曲线y=![]() 的一部分.由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2018,m)与Q(2026,n)均在该抛物线上,则m+n=_____.
的一部分.由点C开始不断重复“A﹣B﹣C”的过程,形成一组波浪线,点P(2018,m)与Q(2026,n)均在该抛物线上,则m+n=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两块全等的直角三角形如图1摆放在一起,设较短直角边为1.现将Rt△BCD沿射线BD方向平移到Rt△B1C1D1的位置(如图2).
(1)求证:四边形ABC1D1是平行四边形;
(2)当四边形ABC1D1为矩形时,求矩形ABC1D1的面积;
(3)当点B的移动距离为多少时,四边形ABC1D1为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,天空中有一个静止的广告气球C,从地面A点测得C点的仰角为45°,从地面B点测得C点的仰角为60°.已知AB=20m,点C和直线AB在同一铅垂平面上,求气球离地面的高度(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE
(Ⅰ)求证:AE是⊙O的切线;
(Ⅱ)若∠DBC=30°,DE=1 cm,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
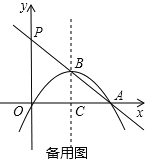
【题目】如图1,抛物线![]() 平移后过点A(8,,0)和原点,顶点为B,对称轴与
平移后过点A(8,,0)和原点,顶点为B,对称轴与![]() 轴相交于点C,与原抛物线相交于点D.
轴相交于点C,与原抛物线相交于点D.
(1)求平移后抛物线的解析式并直接写出阴影部分的面积![]() ;
;
(2)如图2,直线AB与![]() 轴相交于点P,点M为线段OA上一动点,
轴相交于点P,点M为线段OA上一动点,![]() 为直角,边MN与AP相交于点N,设
为直角,边MN与AP相交于点N,设![]() ,试探求:
,试探求:
①![]() 为何值时
为何值时![]() 为等腰三角形;
为等腰三角形;
②![]() 为何值时线段PN的长度最小,最小长度是多少.
为何值时线段PN的长度最小,最小长度是多少.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com