
【题目】如图所示,AB是⊙O的直径,AE是弦,C是劣弧AE的中点,过C作CD⊥AB于点D,CD交AE于点F,过C作CG∥AE交BA的延长线于点G.
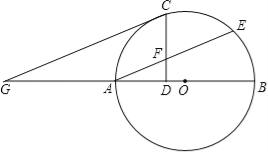
(1)求证:CG是⊙O的切线.
(2)求证:AF=CF.
(3)若∠EAB=30°,CF=2,求GA的长.
【答案】(1)连接OC,由C是劣弧AE的中点,根据垂径定理得OC⊥AE,而CG∥AE,所以CG⊥OC,然后根据切线的判定定理即可得到结论。
(2)连接AC、BC,根据圆周角定理得∠ACB=90°,∠B=∠1,而CD⊥AB,则∠CDB=90°,根据等角的余角相等得到∠B=∠2,所以∠1=∠2,于是得到AF=CF。
(3)2![]()
【解析】试题分析:(1)连结OC,由C是劣弧AE的中点,根据垂径定理得OC⊥AE,而CG∥AE,所以CG⊥OC,然后根据切线的判定定理即可得到结论;
(2)连结AC、BC,根据圆周角定理得∠ACB=90°,∠B=∠1,而CD⊥AB,则∠CDB=90°,根据等角的余角相等得到∠B=∠2,所以∠1=∠2,于是得到AF=CF;
(3)在Rt△ADF中,由于∠DAF=30°,FA=FC=2,根据含30度的直角三角形三边的关系得到DF=1,AD=![]() ,再由AF∥CG,根据平行线分线段成比例得到DA:AG=DF:CF
,再由AF∥CG,根据平行线分线段成比例得到DA:AG=DF:CF
然后把DF=1,AD=![]() ,CF=2代入计算即可.
,CF=2代入计算即可.
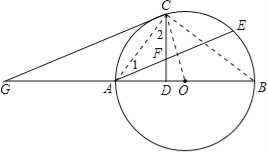
(1)证明:连结OC,如图,
∵C是劣弧AE的中点,
∴OC⊥AE,
∵CG∥AE,
∴CG⊥OC,
∴CG是⊙O的切线;
(2)证明:连结AC、BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠2+∠BCD=90°,
而CD⊥AB,
∴∠B+∠BCD=90°,
∴∠B=∠2,
∵C是劣弧AE的中点,
∴![]() =
=![]() ,
,
∴∠1=∠B,
∴∠1=∠2,
∴AF=CF;
(3)解:在Rt△ADF中,∠DAF=30°,FA=FC=2,
∴DF=![]() AF=1,
AF=1,
∴AD=![]() DF=
DF=![]() ,
,
∵AF∥CG,
∴DA:AG=DF:CF,即![]() :AG=1:2,
:AG=1:2,
∴AG=2![]() .
.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】已知:二次函数![]() ,当
,当![]() 时,函数有最大值5.
时,函数有最大值5.
(1)求此二次函数图象与坐标轴的交点;
(2)将函数![]() 图象x轴下方部分沿x轴向上翻折,得到的新图象与直线
图象x轴下方部分沿x轴向上翻折,得到的新图象与直线![]() 恒有四个交点,从左到右,四个交点依次记为
恒有四个交点,从左到右,四个交点依次记为![]() ,当以
,当以![]() 为直径的圆与
为直径的圆与![]() 轴相切时,求
轴相切时,求![]() 的值.
的值.
(3)若点![]() 是(2)中翻折得到的抛物线弧部分上任意一点,若关于m的一元二次方程
是(2)中翻折得到的抛物线弧部分上任意一点,若关于m的一元二次方程![]() 恒有实数根时,求实数k的最大值.
恒有实数根时,求实数k的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(k+2)x+2k=0.
(1)求证:k取任何实数值,方程总有实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用火柴棒按下列方式搭建三角形:
![]()
三角形个数 | 1 | 2 | 3 | 4 | … |
火柴棒根数 | 3 | 5 | 7 | 9 | … |
(1)当三角形的个数为n时,火柴棒的根数是多少?
(2)求当n=100时,有多少根火柴棒?
(3)当火柴棒的根数为2017时,三角形的个数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】慢车和快车先后从甲地出发沿直线道路匀速驶向乙地,快车比慢车晚出发0.5小时,行驶一段时间后,快车途中休息,休息后继续按原速行驶,到达乙地后停止.慢车和快车离甲地的距离)![]() (千米)与慢车行驶时间
(千米)与慢车行驶时间![]() (小时)之间的函数关系如图所示.
(小时)之间的函数关系如图所示.
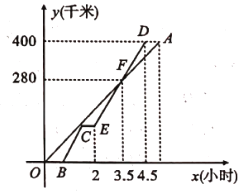
(1)求快车的速度;
(2)求快车到达乙地比慢车到达乙地早了多少小时?
(3)求线段![]() 对应的函数关系式.
对应的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,假命题有( )
①两点之间线段最短;
②到角的两边距离相等的点在角的平分线上;
③过一点有且只有一条直线与已知直线平行;
④垂直于同一直线的两条直线平行;
⑤若![]() 的弦AB,CD交于点P,则
的弦AB,CD交于点P,则![]()
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D,E在△ABC的边BC上,连接AD,AE. ①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:(1)①②![]() ③;(2)①③
③;(2)①③![]() ②;(3)②③
②;(3)②③![]() ①.
①.

(1)以上三个命题是真命题的为(直接答题号) ;
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)当a=2,b=![]() 时,分别求代数式a2﹣2ab+b2和(a﹣b)2的值;
时,分别求代数式a2﹣2ab+b2和(a﹣b)2的值;
(2)当a=﹣5,b=﹣3时,a2﹣2ab+b2 (a﹣b)2(填“=“,“<”“>”)
(3)观察(1)(2)中代探索代数式a2﹣2ab+b2和(a﹣b)2有何数量关系,并把探索的结果写出来:a2﹣2ab+b2 (a﹣b)2(填“=”,“<”“>”)
(4)利用你发现的规律,求135.72﹣2×135.7×35.7+35.72的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com