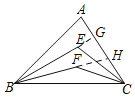
【题目】如图，BE和BF三等分∠ABC，CE和CF三等分∠ACB，∠A＝60°，求∠BEC和∠BFC的度数．
【答案】100°，140°
【解析】
延长BE交AC于G，由三角形外角性质，可得∠BEC＝∠BGC+∠ACE，∠BGC＝∠A+∠ABE，再根据BE和BF三等分∠ABC，CE和CF三等分∠ACB，即可得到∠BEC和∠BFC的度数．
如图，延长BE交AC于G，
由三角形外角性质，可得∠BEC＝∠BGC+∠ACE，∠BGC＝∠A+∠ABE，
∵BE和BF三等分∠ABC，CE和CF三等分∠ACB，
∴∠ABE＝
∠ABC，∠ACE＝∠ACB，
又∵∠ABC+∠ACB＝180°﹣∠A，
∴∠BEC＝∠A+∠ABC+∠ACB＝∠A+（180°﹣∠A）＝60°+
∠A，
当∠A＝60°时，∠BEC＝60°+×60°＝100°，
同理可得，∠BFC＝∠A+（180°﹣∠A）＝120°+∠A＝120°+×60°＝140°．
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，一动点从原点
出发，按向上.向右.向下.向右的方向依次平移，每次移动一个单位，得到
（0，1），
（1，1），
（1，0），
（2，0），…那么点
的坐标为__________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知a,b,c所表示的数在数轴上的位置如图所示:
（1）化简：│a-1│-│c+b│+│b-1│；
（2）若a+b+c=0,且b与-1的距离和c与-1的距离相等，求：-a2+2b-c-(a-4c-b)的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】织金县某中学300名学生参加植树活动，要求每人植4～7棵，活动结束后随机抽查了若干名学生每人的植树量，并分为四种类型，A：4棵；B：5棵；C：6棵；D：7棵．将各类的人数绘制成扇形图（如图1）和条形图（如图2）．
回答下列问题：
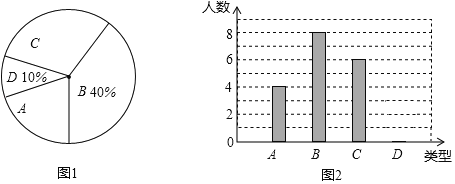
（1）在这次调查中D类型有多少名学生？
（2）写出被调查学生每人植树量的众数、中位数；
（3）求被调查学生每人植树量的平均数，并估计这300名学生共植树多少棵？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】同学们都知道：|5﹣（﹣2）|表示5与﹣2之差的绝对值，实际上也可理解为5与﹣2两数在数轴上所对应的两点之间的距离．请你借助数轴进行以下探索：
（1）数轴上表示5与﹣2两点之间的距离是 ；
（2）数轴上表示x与2的两点之间的距离可以表示为 ；
（3）同理|x+3|+|x﹣1|表示数轴上有理数x所对应的点到﹣3和1所对应的点的距离之和，请你找出所有符合条件的整数x，使得|x+3|+|x﹣1|＝4，这样的整数是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为响应绿色出行号召，越来越多市民选择租用共享单车出行，已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式，如图描述了两种方式应支付金额y(元)与骑行时间x(时)之间的函数关系，根据图象回答下列问题：
(1)求手机支付金额y(元)与骑行时间x(时)的函数关系式；
(2)李老师经常骑行共享单车，请根据不同的骑行时间帮他确定选择哪种支付方式比较合算．
查看答案和解析>>
科目：初中数学 来源： 题型：
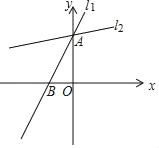
【题目】如图，已知直线l1：y＝2x+4与y轴交于A点，与x轴交于点B，经过A点的直线l2与直线l1所夹的锐角为45°．
（1）过点B作CB⊥AB，交l2于C，求点C的坐标．
（2）求l2的函数解析式．
（3）在直线l1上存在点M，直线l2上存在点N，使得点A、O、M、N四点组成的四边形是平行四边形，请直接写出点N的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
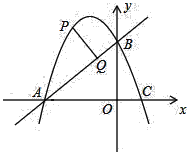
【题目】如图，已知二次函数y＝﹣x2+bx+3的图象与x轴交于A、C两点（点A在点C的左侧），与y轴交于点B，且OA＝OB．
（1）求线段AC的长度；
（2）若点P在抛物线上，点P位于第二象限，过P作PQ⊥AB，垂足为Q．已知PQ＝
，求点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，AB是⊙O的直径，AE是弦，C是劣弧AE的中点，过C作CD⊥AB于点D，CD交AE于点F，过C作CG∥AE交BA的延长线于点G．
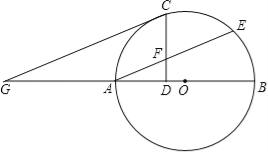
（1）求证：CG是⊙O的切线．
（2）求证：AF=CF．
（3）若∠EAB=30°，CF=2，求GA的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com