
【题目】已知a,b,c所表示的数在数轴上的位置如图所示:
![]()
(1)化简:│a-1│-│c+b│+│b-1│;
(2)若a+b+c=0,且b与-1的距离和c与-1的距离相等,求:-a2+2b-c-(a-4c-b)的值.
科目:初中数学 来源: 题型:
【题目】为扩大内需,国务院决定在全国实施“家电下乡”政策. 第一批列入家电下乡的产品为彩电、冰箱、洗衣机和手机四种产品. 某县一家家电商场,去年第一季度对以上四种产品的销售情况进行了统计,绘制了如下的统计图,请你根据图中信息解答下列问题:

(1)该商场第一季度一共销售了_________台家电;
(2)请补全条形统计图,并求出扇形统计图中彩电所在的扇形圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
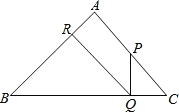
【题目】如图,已知:在△ABC中,∠A=90°,AB=AC=1,P是AC上不与A、C重合的一动点,PQ⊥BC于Q,QR⊥AB于R.
(1)求证:PQ=CQ;
(2)设CP的长为x,QR的长为y,求y与x之间的函数关系式及自变量x的取值范围,并在平面直角坐标系作出函数图象.
(3)PR能否平行于BC?如果能,试求出x的值;若不能,请简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0),下列结论:①ab<0,②b2>4,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0.其中正确结论的个数是( )
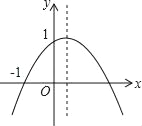
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.
其中说法正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机某天上午全是在东西走向的路上运营,如果规定向东为正,向西为负,他这天行车里程(单位:千米)如下:
-9,+5,-7,+10,+5,-8,-4,+6,-5,-4
(1)将最后一名乘客送达时,他距出发地多远?在出发地什么方向?
(2)如果每行驶1千米耗油0.4升,每升油7元,他一上午的消耗的油花费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]() ,当
,当![]() 时,函数有最大值5.
时,函数有最大值5.
(1)求此二次函数图象与坐标轴的交点;
(2)将函数![]() 图象x轴下方部分沿x轴向上翻折,得到的新图象与直线
图象x轴下方部分沿x轴向上翻折,得到的新图象与直线![]() 恒有四个交点,从左到右,四个交点依次记为
恒有四个交点,从左到右,四个交点依次记为![]() ,当以
,当以![]() 为直径的圆与
为直径的圆与![]() 轴相切时,求
轴相切时,求![]() 的值.
的值.
(3)若点![]() 是(2)中翻折得到的抛物线弧部分上任意一点,若关于m的一元二次方程
是(2)中翻折得到的抛物线弧部分上任意一点,若关于m的一元二次方程![]() 恒有实数根时,求实数k的最大值.
恒有实数根时,求实数k的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com