【题目】如图，平行四边形ABCD中，E、F分别为边AB、DC的中点，则图中共有平行四边形的个数是（ ）．
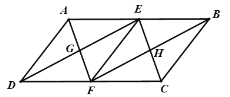
A.3个B.4个C.5个D.6个
【答案】D
【解析】
由在ABCD中，E、F分别为边AB、DC的中点，易得四边形ADFE、四边形AFCE、四边形BCFE、四边形BFDE是平行四边形，进而得出DE∥BF，GE=HF，则四边形GFHE为平行四边形，加上四边形ABCD为平行四边形，则图中共有6个平行四边形．
∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD，
∵E、F分别为边AB、DC的中点，
∴AE=BE=DF=CF，
∴四边形ADFE、四边形AFCE、四边形BCFE、四边形BFDE是平行四边形，
∴DE=BF，DE∥BF，
∴GE=HF，
∴四边形GFHE为平行四边形，
∵四边形ABCD为平行四边形，
∴图中共有6个平行四边形．
故答案为：D．
一线名师权威作业本系列答案科目：初中数学 来源： 题型：
【题目】如图，△OAB和△OCD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝α，AC、BD交于M
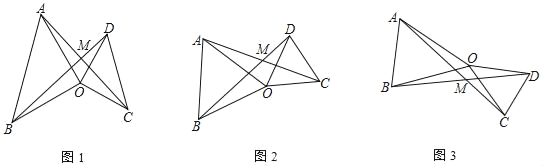
（1）如图1，当α＝90°时，∠AMD的度数为 °
（2）如图2，当α＝60°时，∠AMD的度数为 °
（3）如图3，当△OCD绕O点任意旋转时，∠AMD与α是否存在着确定的数量关系？如果存在，请你用表示∠AMD，并图3进行证明；若不确定，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某工厂生产的某种产品按质量分为10个档次，第1档次（最低档次）的产品一天能生产95件，每件利润6元．每提高一个档次，每件利润增加2元，但一天产量减少5件．
（1）若生产第
档次的产品一天的总利润为
元（其中
为正整数，且1≤
≤10），求出
关于
的函数关系式；
（2）若生产第x档次的产品一天的总利润为1120元，求该产品的质量档次．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图（1），一架云梯AB斜靠在一竖直的墙上，云梯的顶端A距地面15米，梯子的长度比梯子底端B离墙的距离大5米.
（1）这个云梯的底端B离墙多远?
（2）如图（2），如果梯子的顶端下滑了8m（AC的长），那么梯子的底部在水平方向右滑动了多少米?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：①abc＞0；②b＜a+c；③4a-2b+c＞0；④2c＜3b；⑤当m≤x≤m+1时，函数的最大值为a+b+c，则0≤m≤1；其中正确的结论有（ ）
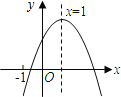
A. 2 个 B. 3 个 C. 4 个 D. 5 个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，一次函数 y=nx+2(n≠0)的图像与反比例函数 y 
(m≠0)在第一象限内的图像交于点 A，与 x 轴交于点 B，线段 OA=5，C 为 x 轴正半轴上一点，且 sin AOC 
.
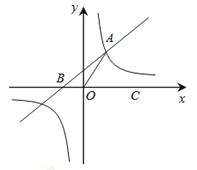
(1)求一次函数和反比例函数的解析式；
(2)求△ AOB 的面积；
(3)请直接写出不等式 nx 2 的解.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了了解学生学习的环境（教室），研究人员对某校一间（坐满学生、门窗关闭）教室中的
的总量进行检测，得到的部分数据如下：
教室连续使用时间 |
|
|
|
|
|
|
|
|
|
|
|
经研究发现，该教室空气中总量
是教室连使用时间
的一次函数．
（1）请直接写出
与的函数关系式；
（2）根据有关资料推算，当该教室空气中总量达到
时，学生将会稍感不适，则该教室连续使用__________
学生将会开始稍感不适．
（3）如果该教室在连续使用
分钟时开门通风，在学生全部离开教室的情况下，
分钟可将教室空气中的总量减少到
，求开门通风时教室空气中平均每分钟减少多少立方米？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
