Question

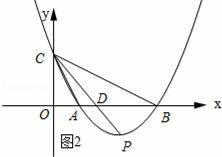
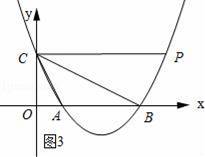
如图，在平面直角坐标系xOy中，抛物线y=ax²+bx+c与x轴交于A（1，0），B（4，0）两点，与y轴交于点C（0，2）．

（1）求抛物线的表达式；

（2）求证：∠CAO=∠BCO；

（3）若点P是抛物线上的一点，且∠PCB+∠ACB=∠BCO，求直线CP的表达式．

Answer 1

【考点】二次函数综合题．

【分析】（1）设抛物线的解析式为为y=a（x﹣1）（x﹣4），将点C的坐标代可求得a的值，从而得到抛物线的解析式；

（2）先证明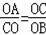，从而可证明△AOC∽△COB，由相似三角形的性质可证得∠CAO=∠BCO；

（3）先证明∠PCB=∠CBO，如图2所示可得到CD=BD，然后由勾股定理可求得OD的长，从而得到点D的坐标，由点C和点D的坐标可求得PC的解析式，如图3所示当∠PCB=∠CBO时，PC∥OB，从而可得到PC的解析式．

【解答】解：（1）设抛物线的解析式为y=a（x﹣1）（x﹣4）．

∵将C（0，2）代入得：4a=2，解得a=，

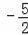
∴抛物线的解析式为y=（x﹣1）（x﹣4），即y=x²x+2．

（2）如图1所示：连接AC．

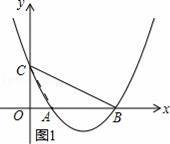
∵由题意可知；OA=1，OC=2，OB=4，

∴．

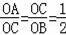
又∵∠COA=∠BOC，

∴△AOC∽△COB．

∴∠CAO=∠BCO．

（3）①如图2所示：

∵∠PCB+∠ACB=∠BCO，∠ACO+∠ACB=∠BCO，

∴∠PCB=∠ACO．

∵△AOC∽△COB，

∴∠ACO=∠CBO．

∴∠PCB=∠CBO．

∴CD=BD．

设OD=x，则DBCD=4﹣x．

在Rt△DCO中，由勾股定理得：OD²+CO²=DC²，即x²+2²=（4﹣x）²．解得：x=1.5．

∴点D的坐标为（1.5，0）．

设直线CP的解析式为y=kx+b．

∵将（0，2），D（1.5，0）代入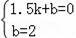得：，解得：，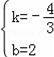

∴直线CP的解析式为y=﹣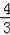x+2．

如图3所示：

∵∠PCB+∠ACB=∠BCO，∠ACO+∠ACB=∠BCO，

∴∠PCB=∠ACO．

∵△AOC∽△COB，

∴∠ACO=∠CBO．

∴∠PCB=∠CBO．

∴CP∥OB．

∴CP的解析式为y=2．

综上所述，直线CP的解析式为y=﹣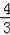x+2或y=2．

【点评】本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系数法求一次函数和二次函数的解析式、相似三角形的性质和判定、勾股定理的应用，证得DC=DB，然后依据勾股定理求得OD的长是解题的关键．