Question

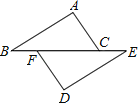
【题目】如图，点B，F，C，E在一条直线上BF＝CE，AC＝DF．

（1）在下列条件 ①∠B＝∠E；②∠ACB＝∠DFE；③AB＝DE；④AC∥DF中，只添加一个条件就可以证得△ABC≌△DEF，则所有正确条件的序号是　 　．

（2）根据已知及（1）中添加的一个条件证明∠A＝∠D．

Answer 1

【答案】（1）②③④；（2）添加条件∠ACB＝∠DFE，理由详见解析．

【解析】

（1）由全等三角形的判定方法即可得出答案；

（2）答案不唯一，添加条件∠ACB＝∠DFE，证明△ABC≌△DEF（SAS）；即可得出∠A＝∠D．

解：（1）①在△ABC和△DEF中，BC＝EF，AC＝DF，∠B＝∠E，

不能判定△ABC和△DEF全等；

②∵BF＝CE，

∴BF+CF＝CE+CF，

即BC＝EF，

在△ABC和△DEF中，，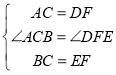

∴△ABC≌△DEF（SAS）；

③在△ABC和△DEF中，，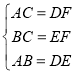

∴△ABC≌△DEF（SSS）；

④∵AC∥DF，

∴∠ACB＝∠DFE，

在△ABC和△DEF中，，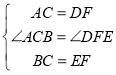

∴△ABC≌△DEF（SAS）；

故答案为：②③④；

（2）答案不惟一．添加条件∠ACB＝∠DFE，理由如下：

∵BF＝EC，

∴BF+CF＝EC+CF．

∴BC＝EF．

在△ABC和△DEF中，，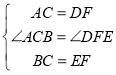

∴△ABC≌△DEF（SAS）；

∴∠A＝∠D．