
【题目】函数![]() 和
和![]() 在第一象限内的图象如图所示,点
在第一象限内的图象如图所示,点![]() 是
是![]() 的图象上一动点,作
的图象上一动点,作![]() 轴于点
轴于点![]() ,交
,交![]() 的图象于点
的图象于点![]() ,作
,作![]() 轴于点
轴于点![]() ,交
,交![]() 的图象于点
的图象于点![]() ,给出如下结论:①
,给出如下结论:①![]() 与
与![]() 的面积相等;②
的面积相等;②![]() 与
与![]() 始终相等;③四边形
始终相等;③四边形![]() 的面积大小不会发生变化;④
的面积大小不会发生变化;④![]() ,其中正确的结论序号是( )
,其中正确的结论序号是( )
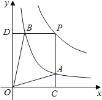
A. ①②③ B. ②③④ C. ①③④ D. ①②④
【答案】C
【解析】
设点P的坐标为(m,![]() )(m>0),则A(m,
)(m>0),则A(m,![]() ),C(m,0),B(
),C(m,0),B(![]() ,
,![]() )D(0,
)D(0,![]() ).①根据反比例函数系数k的几何意义即可得出S△ODB=S△OCA,该结论正确;②由点的坐标可找出PA=
).①根据反比例函数系数k的几何意义即可得出S△ODB=S△OCA,该结论正确;②由点的坐标可找出PA=![]() ,PB=
,PB=![]() ,由此可得出只有m=2是PA=PB,该结论不成;③利用分割图形法求图形面积结合反比例系数k的几何意义即可得知该结论成立;④结合点的坐标即可找出PA=
,由此可得出只有m=2是PA=PB,该结论不成;③利用分割图形法求图形面积结合反比例系数k的几何意义即可得知该结论成立;④结合点的坐标即可找出PA=![]() ,AC=
,AC=![]() ,由此可得出该结论成立.综上即可得出正确的结论为①③④.
,由此可得出该结论成立.综上即可得出正确的结论为①③④.
解:设点P的坐标为(m,![]() )(m>0),则A(m,
)(m>0),则A(m,![]() ),C(m,0),B(
),C(m,0),B(![]() ,
,![]() ),D(0,
),D(0,![]() ).
).
①S△ODB=![]() ×1=
×1=![]() ,S△OCA=
,S△OCA=![]() ×1=
×1=![]() ,
,
∴△ODB与△OCA的面积相等,①成立;
②PA=![]() -
-![]() =
=![]() ,PB=m-
,PB=m-![]() =
=![]() ,
,
令PA=PB,即![]() =
=![]() ,
,
解得:m=2.
∴当m=2时,PA=PB,②不正确;
③S四边形PAOB=S矩形OCPD-S△ODB-S△OCA=4-![]() -
-![]() =3.
=3.
∴四边形PAOB的面积大小不会发生变化,③正确;
④∵PA=![]() -
-![]() =
=![]() ,AC=
,AC=![]() -0=
-0=![]() ,
,
∵![]() =3×
=3×![]() ,
,
∴PA=3AC,④正确.
综上可知:正确的结论有①③④.
故选:C.


科目:初中数学 来源: 题型:
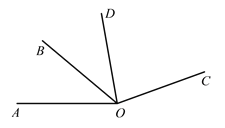
【题目】几何计算:
如图,已知∠AOB=40°,∠BOC=3∠AOB,OD平分∠AOC,求∠COD的度数.
解:因为∠BOC=3∠AOB,∠AOB=40°
所以∠BOC=__________°
所以∠AOC=__________ + _________
=__________° + __________°
=__________°
因为OD平分∠AOC
所以∠COD=![]() __________=__________°
__________=__________°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E.F分别在AB、CD上,AE=CF,连接AF,BF,DE,CE,分别交于H、G.
求证:(1)四边形AECF是平行四边形。(2)EF与GH互相平分。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点A(1,4)和点B
的图象交于点A(1,4)和点B
(![]() ,
,![]() ).
).

(1)求这两个函数的表达式;
(2)观察图象,当![]() >0时,直接写出
>0时,直接写出![]() >
>![]() 时自变量
时自变量![]() 的取值范围;
的取值范围;
(3)如果点C与点A关于![]() 轴对称,求△ABC的面积.
轴对称,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式: ![]() ,
, ![]() ,给出定义如下:
,给出定义如下:
我们称使等式![]() 成立的一对有理数
成立的一对有理数![]() ,
, ![]() 为“共生有理数对”,记为(
为“共生有理数对”,记为(![]() ,
, ![]() ),如:数对(
),如:数对(![]() ,
, ![]() ),(
),(![]() ,
, ![]() ),都是“共生有理数对”.
),都是“共生有理数对”.
(1)判断数对(![]() ,
, ![]() ),(
),(![]() ,
, ![]() )是不是“共生有理数对”,写出过程;
)是不是“共生有理数对”,写出过程;
(2)若(![]() ,
, ![]() )是“共生有理数对”,求
)是“共生有理数对”,求![]() 的值;
的值;
(3)若(![]() ,
, ![]() )是“共生有理数对”,则(
)是“共生有理数对”,则(![]() ,
, ![]() ) “共生有理数对”(填“是”或“不是”);说明理由;
) “共生有理数对”(填“是”或“不是”);说明理由;
(4)请再写出一对符合条件的 “共生有理数对”为 (注意:不能与题目中已有的“共生有理数对”重复)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.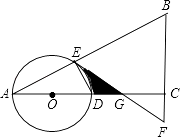
(1)试判断直线EF与⊙O的位置关系,并说明理由;
(2)若OA=2,∠A=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°),放置在一凹槽内,三个顶点A,B,C分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=5cm,BE=7cm,求该三角形零件的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,A(-1,5)、B(-1,0),C(-4,3).
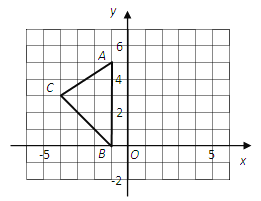
(1)△ABC的面积是 .
(2)在下图中画出△ABC向下平移2个单位,向右平移5个单位后的△A1B1C1.
(3)写出点A1、B1、C1的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com