
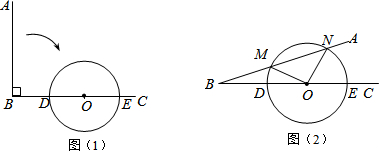
分析 (1)要求当射线BA绕点B按顺时针方向旋转多少度时与⊙O相切,就要先利用切线的性质画出图形,从图中可以看出旋转的度数就是∠A′BC的度数.然后利用图形来计算.从图中可看出,OG=OB的一半,所以角PBG=30°,所以当射线BA绕点B按顺时针方向旋转60°或120°时与⊙O相切;
(2)由勾股定理边的关系可知弧所对的圆心角是一个直角,然后利用弧长公式计算.
解答 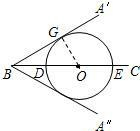 解:(1)当射线BA绕点B按顺时针方向旋转60°或120°时与⊙O相切,
解:(1)当射线BA绕点B按顺时针方向旋转60°或120°时与⊙O相切,
理由:当BA绕点B按顺时针方向旋转60°到BA′的位置,则∠A′BO=30°,
过O作OG⊥BA′垂足为G,
∴OG=$\frac{1}{2}$OB=2,
∴BA′是⊙O的切线,
同理,当BA绕点B按顺时针方向旋转120度到BA″的位置时,
BA″也是⊙O的切线.
∵OG=$\frac{1}{2}$OB,
∴∠A′BO=30°,
∴BA绕点B按顺时针方向旋转了60°,
同理可知,当BA绕点B按顺时针方向旋转到BA″的位置时,BA与⊙O相切,BA绕点B按顺时针方向旋转了120°;
(2)∵MN=2$\sqrt{2}$,OM=ON=2,
∴MN2=OM2+ON2,
∴∠MON=90°,
∴$\widehat{MN}$的长为$\frac{90π×2}{180}$=π.
点评 此题主要考查了切线的判定、垂径定理、解直角三角形以及扇形面积的计算方法,难度不大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
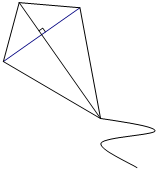 如图,小明将一根长为1.4米的竹条截为两段,并互相垂直固定,作为风筝的龙骨,制作成了一个面积为0.24米2的风筝.请你计算一下将竹条截成长度分别为多少的两段?
如图,小明将一根长为1.4米的竹条截为两段,并互相垂直固定,作为风筝的龙骨,制作成了一个面积为0.24米2的风筝.请你计算一下将竹条截成长度分别为多少的两段?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
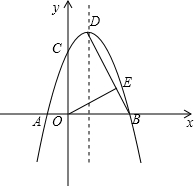 如图,抛物线y=-x2+bx+c与x轴交于A、B点,与y轴交于C点,顶点为D,其中点A、C的坐标分别是(-1,0)、(0,3).
如图,抛物线y=-x2+bx+c与x轴交于A、B点,与y轴交于C点,顶点为D,其中点A、C的坐标分别是(-1,0)、(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
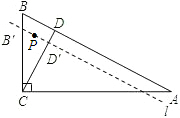 如图,在Rt△ABC中,∠ACB=90°,AC=$6\sqrt{3}$cm,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=$6\sqrt{3}$cm,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com