
| A. | 36 | B. | 38 | C. | 34 | D. | 28 |
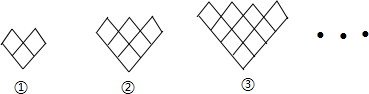
分析 由题意可知:第①个图形含边长为1的菱形1+2=3个,第②个图形含边长为1的菱形1+2+3=6个,第③个图形含边长为1的菱形1+2+3+4=10个,…,按此规律,则第n个图形中含边长为1的菱形的个数为1+2+3+4+…+n+(n+1)=$\frac{1}{2}$(n+1)(n+2),由此代入求得答案即可.
解答 解:∵第①个图形含边长为1的菱形1+2=3个,
第②个图形含边长为1的菱形1+2+3=6个,
第③个图形含边长为1的菱形1+2+3+4=10个,
…,
∴第n个图形中含边长为1的菱形的个数为1+2+3+4+…+n+(n+1)=$\frac{1}{2}$(n+1)(n+2),
∴第⑦个图形中含边长为1的菱形的个数为1+2+3+4+5+6+7+8=36.
故选:A.
点评 此题主要考查了图形变化规律,根据图形的联系得出菱形的个数变化规律是解题关键.


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
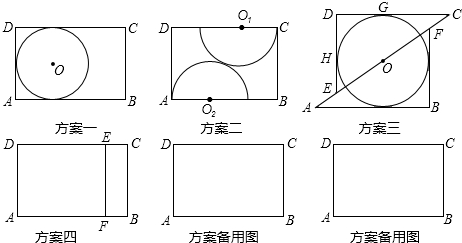
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 对于一个三角形,设其三个内角的度数分别为x°、y°和z°,若x、y、z满足x2+y2=z2,我们定义这个三角形为美好三角形.
对于一个三角形,设其三个内角的度数分别为x°、y°和z°,若x、y、z满足x2+y2=z2,我们定义这个三角形为美好三角形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于F,则$\frac{DF}{AD}$=( )
如图,在△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于F,则$\frac{DF}{AD}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com