
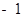 ),且P(
),且P(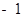 ,-2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.
,-2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B. 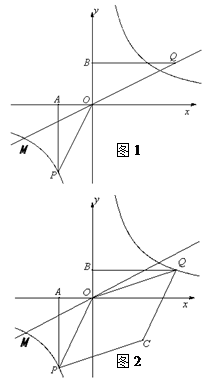
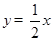 ,
,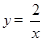 (2)
(2)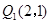 和
和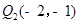 (3)
(3) ,
,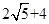
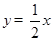 ---------------1分
---------------1分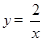 ---------------2分
---------------2分 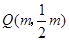 , ----------------------3分
, ----------------------3分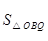 =
=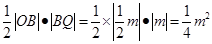
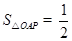 ×1×2=1
×1×2=1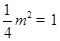 ,解得
,解得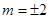 --------------------6分
--------------------6分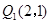 和
和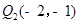 -------------------7分
-------------------7分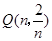 ,
,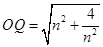 -------------------8分
-------------------8分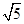 ,所以平行四边形OPCQ周长是
,所以平行四边形OPCQ周长是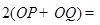
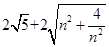 .····················· 10分
.····················· 10分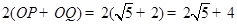 .-------11分
.-------11分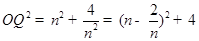
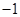 ,
,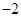 )是定点,所以OP的长也是定长,所以要求平行四边形OPCQ周长的最小值就只需求OQ的最小值.
)是定点,所以OP的长也是定长,所以要求平行四边形OPCQ周长的最小值就只需求OQ的最小值.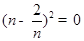 即
即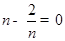 时,
时,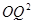 有最小值4,
有最小值4,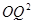 同时取得最小值,所以OQ有最小值2.
同时取得最小值,所以OQ有最小值2.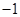 ,
,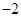 )是定点,所以OP的长也是定长,所以要求平行四边形OPCQ周长的最小值就只需求OQ的最小值,所以当
)是定点,所以OP的长也是定长,所以要求平行四边形OPCQ周长的最小值就只需求OQ的最小值,所以当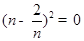 即
即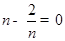 时,
时,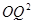 有最小值4,又因为OQ为正值,所以OQ与
有最小值4,又因为OQ为正值,所以OQ与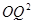 同时取得最小值,所以OQ有最小值2.
同时取得最小值,所以OQ有最小值2.

科目:初中数学 来源:不详 题型:解答题
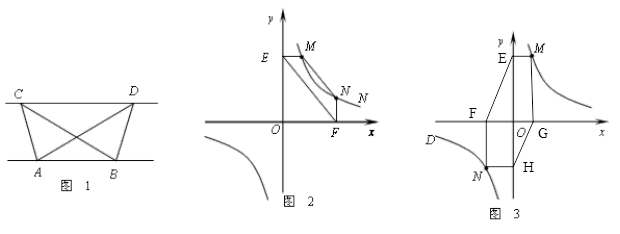
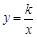 (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F. 试证明:MN∥EF.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F. 试证明:MN∥EF. 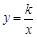 (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,过点M作MG⊥x轴,过点N作NH⊥y轴,垂足分别为E、F、G、H. 试证明:EF ∥GH.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,过点M作MG⊥x轴,过点N作NH⊥y轴,垂足分别为E、F、G、H. 试证明:EF ∥GH.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
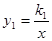 (其中k1>0)和
(其中k1>0)和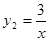 在第一象限内的图象依次是C1和 C2,点P在C1上。矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF垂直x轴于F点,且图中阴影部分面积为13,则EF﹕AC为( )
在第一象限内的图象依次是C1和 C2,点P在C1上。矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF垂直x轴于F点,且图中阴影部分面积为13,则EF﹕AC为( )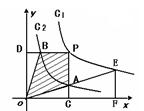
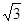 D.2﹕
D.2﹕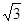
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com