
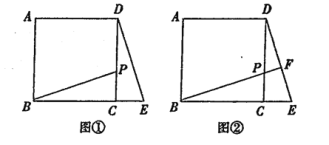
【题目】探究:如图①,在正方形ABCD中,点P在边CD上(不与点C、D重合),连结BP.将△BCP绕点C顺时针旋转至△DCE,点B的对应点是点D,旋转的角度是 度.
应用:将图①中的BP延长交边DE于点F,其它条件不变,如图②.求∠BFE的度数.
拓展:如图②,若DP=2CP,BC=3,则四边形ABED的面积是 .
【答案】(1)90°;(2)![]() .
.
【解析】
探究:根据旋转的定义找到旋转角即可;
应用:由△BCP≌△DCE,可得∠CBP=∠CDE,由于∠CDE+∠E=90°,所以∠CBP+∠E=90°,所以∠BFE=90°;
拓展:由DC=BC=3,DP=2CP,可得CP=1,所以CE=1,所以四边形ABED面积=正方形ABCD面积+△DCE面积,可求.
探究:根据旋转角的定义可知∠DCE是旋转角为90°,
故答案为90;
应用:∵△BCP绕点C顺时针旋转至△DCE,
∴△BCP≌△DCE(SSS).
∴∠CBP=∠CDE.
∵∠CDE+∠E=90°,
∴∠CBP+∠E=90°.
∴∠BFE=90°;
拓展:∵DC=BC=3,DP=2CP,
∴CP=1.
∴CE=1.
所以四边形ABED面积=正方形ABCD面积+△DCE面积=9+![]() ×1×3=10.5.
×1×3=10.5.
故答案为90;10.5.


科目:初中数学 来源: 题型:
【题目】把![]() 按下列要求进行操作:若指数为奇数则乘以
按下列要求进行操作:若指数为奇数则乘以![]() ,若指数为偶数则把它的指数除以2,如此继续下去,则第几次操作时
,若指数为偶数则把它的指数除以2,如此继续下去,则第几次操作时![]() 的指数为4?第10次操作时
的指数为4?第10次操作时![]() 的指数是多少?你有什么发现?
的指数是多少?你有什么发现?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
如果函数y=f(x)满足:对于自变量x的取值范围内的任意x1,x2,
(1)若![]() ,都有
,都有![]() ,则称f(x)是增函数;
,则称f(x)是增函数;
(2)若![]() ,都有
,都有![]() ,则称f(x)是减函数.
,则称f(x)是减函数.
例题:证明函数f(x)=![]() 是减函数.
是减函数.
证明:设![]() ,
,
![]()
∵![]() ,
,
∴![]() .
.
∴![]() .即
.即![]() .
.
∴![]() .
.
∴函数![]() 是减函数.
是减函数.
根据以上材料,解答下面的问题:
已知函数f(x)=![]() (x<0),例如f(-1)=
(x<0),例如f(-1)=![]() =-3,f(-2)=
=-3,f(-2)=![]() =-
=-![]()
(1)计算:f(-3)= ;
(2)猜想:函数f(x)=![]() (x<0)是 函数(填“增”或“减”);
(x<0)是 函数(填“增”或“减”);
(3)请仿照例题证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,求三角形各边的长;
(2)能围成有一边的长是4cm的等腰三角形吗?若能,求出其他两边的长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
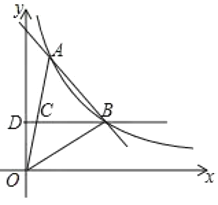
【题目】如图,一次函数y=ax+b与反比例函数y=![]() (x>0)的图像在第一象限交于A、B两点,点B坐标为(4,2),连接OA、OB,过点B作BD⊥y轴,垂足为D,交OA于点C,且OC=CA.
(x>0)的图像在第一象限交于A、B两点,点B坐标为(4,2),连接OA、OB,过点B作BD⊥y轴,垂足为D,交OA于点C,且OC=CA.
(1)求反比例函数和一次函数的表达式;
(2)根据图像直接说出不等式ax+b-![]() <0的解集为______;
<0的解集为______;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
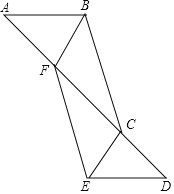
【题目】如图,在△ABC和△DEF中,AB∥DE,点A,F,C,D在同一直线上,AF=CD,∠AFE=∠BCD.
试说明:
(1)△ABC≌△DEF;
(2)BF∥EC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进西装30件,衬衫45件,共用了39000元,其中西装的单价是衬衫的5倍。
(1)求西装和衬衫的单价各为多少元?
(2)商场仍需要购买上面的两种产品55件(每种产品的单价不变),采购部预算共支出32000元,财会算了一下,说:“如果你用这些钱共买这两种产品,那么账肯定算错了”请你用学过的方程知识解释财会为什么会这样说?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点E为矩形ABCD边AD上一点,点P,点Q同时从点B出发,点P沿BE→ED→DC 运动到点C停止,点Q沿BC运动到点C停止,它们运动的速度都是1/s,设P,Q出发t秒时,△BPQ的面积为y,已知y与t的函数关系的图形如图2(曲线OM为抛物线的一部分),则下列结论::①AD=BE=5;②当0<t≤5时; ![]() ;③直线NH的解析式为y=-
;③直线NH的解析式为y=-![]() t+27;④若△ABE与△QBP相似,则t=
t+27;④若△ABE与△QBP相似,则t=![]() 秒. 其中正确的结论个数为( )
秒. 其中正确的结论个数为( )


A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com