
����Ŀ����ƽ��ֱ������ϵxOy�У���һ��C������C�ֱ���CA��x�ᣬCB��y�ᣬ��A��B�Ǵ��㣮
���壺��������OACB���ܳ����������ֵ��ȣ����C��ƽ��ֱ������ϵ�е�ƽ��㣮
��1�����ж�������ƽ��ֱ������ϵ�е�ƽ��������������ţ�
��E��1��2����F����4��4��
��2�����ڵ�һ��������һ��ƽ���N��4��m��ǡ����һ�κ���y=��x+b��bΪ��������ͼ���ϣ�
����m��b��ֵ��
��һ�κ���y=��x+b��bΪ��������y�ύ�ڵ�D���ʣ����⺯��ͼ���ϣ��Ƿ���ڵ�M��ʹS��OMD=3S��OND �� �����ڣ���ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�
��3������P��0����2������ƽ����x���ֱ������ƽ���Q�����У������ƽ���Q�����ꣻ��û�У�˵�����ɣ�
���𰸡�
��1����
��2��
�⣺�١�N�ǵ�һ�����е�ƽ��㣬
��4m=2��4+m�������m=4��
��N��4��4����
��N����y=��x+b��ͼ���ϣ�
��4=��4+b�����b=8��
���ɢٿ�֪һ�κ�������ʽΪy=��x+8��
��D��0��8����
��OD=8����N��4��4����
��S��OND= ![]() ��4��8=16��
��4��8=16��
��S��OMD=3S��OND=3��16=48��
��M����Ϊ��t����t+8������M��y��ľ���Ϊ|t|��
�� ![]() ��8��|t|=48�����t=12��t=��12��
��8��|t|=48�����t=12��t=��12��
��t=12ʱ����t+8=��4����t=��12ʱ����t+8=20��
��������������ĵ�M��������Ϊ��12����4����12��20����
��3��
�⣺��PQ��x�ᣬ��P��0����2����
������Q������x����2����
�ߵ�QΪƽ��㣬
��2|x|=2��|x|+2�����÷����⣬
���������������Q�㣮
���������⣺��1����1��2��2����|��1|+2����4��4=2����|��4|+4����
���E����ƽ��㣬��N��ƽ��㣬
���Դ��ǣ��ڣ�
�����㾫��������һ�κ��������ʶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪һ��أ�һ�κ���y=kx+b���������ʣ���1����k>0ʱ��y��x�����������2����k<0ʱ��y��x���������С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�� 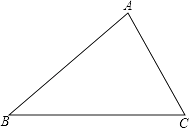
��1���ó߹���ͼ�ķ����ֱ�������ABC�Ľ�ƽ����BE��CF����BE��CF���ڵ�O����������ͼ�ۼ�����Ҫ��д����������
��2���ڣ�1���У������ABC=40�㣬��ACB=60�㣬���BOC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ʽ��32��12=8=8��1��52��32=16=8��2��72��52=24=8��3��92��72=32=8��4�����۲�����һϵ�е�ʽ�����ܷ���ʲô���ɣ���n��n��1����ʾ��Ȼ�����ù���n�ĵ�ʽ��ʾ�������Ϊ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У�AB=AC��D��E��б��BC�����㣬����DAE=45��������ADC�Ƶ�A˳ʱ����ת90���õ���AFB������EF�����н��ۣ��١�AED�ա�AEF����AE��BE=AD��CD���ۡ�ABC����������ı���AFBD���������BE2+DC2=DE2��BE+DC=DE������ȷ���ǣ� ��
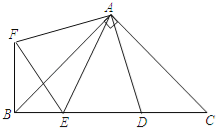
A. �٢ڢ� B. �ۢܢ� C. �٢ۢ� D. �٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,AC��BC,CΪ����,CD��AB,DΪ����,BC=8,CD=4.8,BD=6.4,AD=3.6,AC= 6,��ô��C��AB�ľ�����_______,��A��BC�ľ�����________,��B��CD �ľ�����_____,A��B����ľ�����_________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���� m ������ʵ������� M��1+m��-1���ڵڣ� ������
A.һB.��C.��D.��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��֯ȥ���ο�����ض�ͯ��Ϊ������ȥһЩͼ�飬ÿ�˷�8��ͼ�飬����5����ÿ�˷�7��ͼ�飬����6������ô����ض�ͯ�У�������
A.10��B.11��C.12��D.13��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
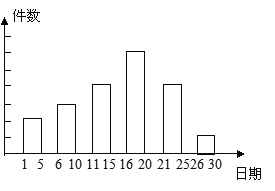
����Ŀ������У�ٰ�Ŀ����У���һ����С��������.��Ʒ�Ͻ�ʱ��Ϊ3��1����30�գ���ί���ͬѧ�ǽ�������Ʒ��ʱ��˳��ÿ5�����һ�飬��ÿһ��ļ�������ͳ�ƣ����Ƴ���ͼ��ʾ��ͳ��ͼ.��֪�����Ҹ����εĸ߶ȱ�Ϊ2:3:4:6:4:1. ������ļ�����12��. ����ش�
(1)���λ����________����Ʒ������������Ʒ��������λ����________��.
(2)�����ȣ�������͵�����ֱ���10����2����Ʒ����ô����Ϊ���������ĸ�����ʽϸߣ�Ϊʲô��
С�������Ƚ�������ί�������4�����������ƷA��B��C��D��ѡ����������ȫУչʾ��������״ͼ���б�������պ�չʾB��D�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������εij�Ϊa cm����Ϊb cm������������2cm�������ԭ�������� cm2 ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com