练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．观察下列各式：
    13=12
    13+23=32
    13+23+33=62
    13+23+33+43=102…
    （1）计算：13+23+33…+183+193+203=2102
    （2）用含自然数n的等式表示上述各式的规律13+23+33…+（n-1）3+n3=（$\frac{n（n+1）}{2}$）2．

    分析 仔细观察数轴的变化，找到变化的规律，利用规律解题即可．

    解答 解：∵13=12
    13+23=（1+2）2=32
    13+23+33=（1+2+3）2=62
    13+23+33+43=（1+2+3+4）2=102…
    ∴（1）计算：13+23+33…+183+193+203=（1+2+3+4+…+20）2=2102，
    （2）用含自然数n的等式表示上述各式的规律为13+23+33…+（n-1）3+n3=（$\frac{n（n+1）}{2}$）2．
    故答案为：2102，13+23+33…+（n-1）3+n3=（$\frac{n（n+1）}{2}$）2．

    点评 本题考查了数字的变化类问题及有理数的混合运算的知识，解题的关键是能够仔细观察题目变化，找到规律，难度不大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

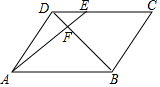    5．如图，?ABCD中，点E是边DC的一个三等分点，AE交对角线BD于点F，则S△DEF：S△DAF等于（　　）
    A．1：2B．2：3C．1：4D．1：3

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．若3m=2，3n=4，则32m+n+1=48．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．计算：（-a）4÷（-a）=-a3；0.252007×（-4）2008=4；（-x）2•x3=x5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．计算
    （1）（-1）2015+（$\frac{1}{2}$）-2-（3.14-π）0
    （2）（2x3y）2•（-2xy）+（-2x3y）3÷（2x2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．△ABC中，∠C=90°，若b=6，∠B=30°，则a=6$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．计算（-2a）2•a3，正确的是（　　）
    A．2a5B．-4a5C．4a5D．4a6

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图所示是一块长、宽、高分别为3cm、4cm、6cm的长方体纸箱（纸箱厚度忽略不计）
    （1）求长方体底面的对角线长．
    （2）若揭开盖子EFGH后，捕入一根长为10cm的细木棒，则细木棒露在外面的最短长度是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

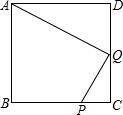    12．如图：正方形ABCD中，P是BC上的点，BP=3PC，Q是CD的中点．
    （1）求证：△ADQ∽△QCP；
    （2）已知∠QPC=55°，求∠QAD的度数．

    查看答案和解析>>

    同步练习册答案