
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,![]() 的顶点均在格点上.
的顶点均在格点上.
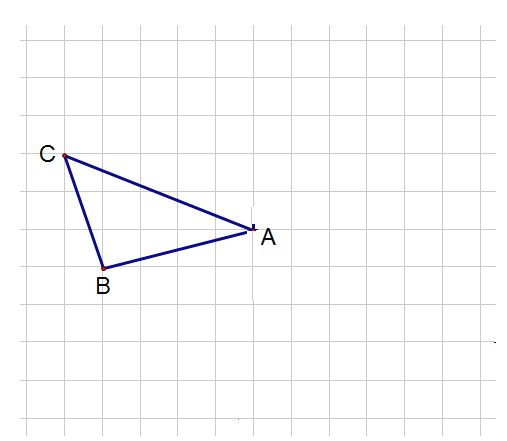
(1)请建立合适的平面直角坐标系,使点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() 和
和![]() ,并写出点
,并写出点![]() 的坐标为___________;
的坐标为___________;
(2)在(1)的条件下.①![]() 中任意一点
中任意一点![]() 经平移后对应点
经平移后对应点![]() ,将
,将![]() 作同样的平移得到
作同样的平移得到![]() ,请画出
,请画出![]() ,并直接写出点
,并直接写出点![]() 的坐标;
的坐标;
②点![]() 在
在![]() 轴上,且
轴上,且![]() ,则点
,则点![]() 的坐标为__________.
的坐标为__________.
【答案】(1)坐标系见解析,![]() ;(2)①作图见解析,
;(2)①作图见解析,![]() ;②
;②![]() 或
或![]()
【解析】
(1)如下图,根据点A和点B的坐标可确定坐标系并得出C的坐标;
(2)①根据点P和点![]() 可知平移方式为向右平移2个单位,向下平移4个单位,对△ABC进行如此变换可得;
可知平移方式为向右平移2个单位,向下平移4个单位,对△ABC进行如此变换可得;
②点D存在2种情况,一种是在点A的上方,一种是在点A的下方,以AD为底,点B到y轴的距离为高,根据面积可求得AD的距离,从而得出点D.
(1)坐标系如下图:
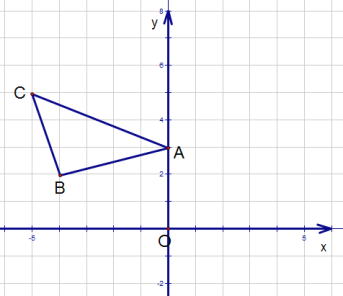
C![]()
(2)①∵点![]() 经平移后对应点
经平移后对应点![]()
∴平移过程为向右平移2个单位,向下平移4个单位,图形如下

∴![]()
![]()
(3)情况一:点D在点A的上方,图形如下:

∵B![]()
∴点B到y轴的距离为4
∵![]()
∴![]()
∴AD=4
∵A![]() ,∴D(0,7)
,∴D(0,7)
情况二:当点D在点A的下方
同理AD=4,∴D(0,-1)


科目:初中数学 来源: 题型:
【题目】有5张看上去无差别的卡片,上面分别写着0,π, ![]() ,
, ![]() ,1.333,背面朝上放在不透明的桌子上,若随机抽取1张,则取出的卡片上的数是无理数的概率是( )
,1.333,背面朝上放在不透明的桌子上,若随机抽取1张,则取出的卡片上的数是无理数的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题: 某校为美化校园,计划对一些区域进行绿化,安排了甲、乙两个工程队完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且两队在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天,求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂准备翻建新的大门,厂门要求设计成轴对称的拱形曲线.已知厂门的最大宽度AB=12m,最大高度OC=4m,工厂的运输卡车的高度是3m,宽度是5.8m.现设计了两种方案.方案一:建成抛物线形状(如图1);方案二:建成圆弧形状(如图2).为确保工厂的卡车在通过厂门时更安全,你认为应采用哪种设计方案?请说明理由.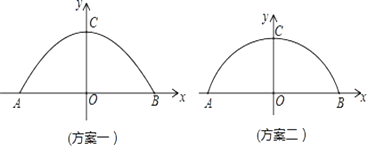
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,不能判断四边形ABCD是平行四边形的为( )
A. AB∥CD,AD∥BC
B. AB=CD,AD=BC
C. AB∥CD,AD=BC
D. AB∥CD,AB=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们在学习“实数”时,画了这样一个图,以数轴上的单位长为1的线段作一个正方形,然后以原点O为圆心,正方形的对角线长为半径画弧交x轴于点A,请根据图形回答下列问题:
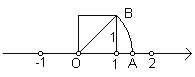
(1)线段OA的长度是___________
(2)这种研究和解决问题的方式,体现了的数学思想方法( ).
A.数形结合B.归纳C.换元D.消元
(3)计算:![]() ﹣
﹣![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于点Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E、G、H分別在矩形ABCD的边AB、CD、DA上,AH=2.
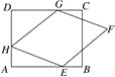
(1)已知DG=6,求AE的长;
(2)已知DG=2,求证:四边形EFGH为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲处表示两条路的交叉口,乙处也是两条路的交叉口,如果用(1,3)表示甲处的位置,那么“(1,3)→(2,3)→(3,3)→(4,3)→(4,2)→(4,1)→(4,0)”表示甲处到乙处的一种路线,若图中一个单位长度表示5Km,请你用上述表示法写出甲处到乙处的另两种走法,最短距离是多少千米?
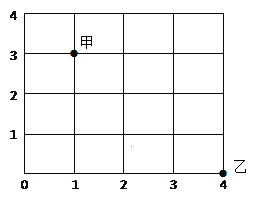
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com