
【题目】某工厂准备翻建新的大门,厂门要求设计成轴对称的拱形曲线.已知厂门的最大宽度AB=12m,最大高度OC=4m,工厂的运输卡车的高度是3m,宽度是5.8m.现设计了两种方案.方案一:建成抛物线形状(如图1);方案二:建成圆弧形状(如图2).为确保工厂的卡车在通过厂门时更安全,你认为应采用哪种设计方案?请说明理由.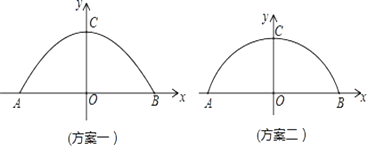
【答案】解:第一方案:设抛物线的表达式是y=a(x+6)(x6),
因C(0,4)在抛物线的图象上,代入表达式,得a= ![]() .
.
故抛物线的表达式是y= ![]() x2+4.
x2+4.
把第一象限的点(t,3)代入函数,得3= ![]() t2+4,
t2+4,
∴t=3,
∴当高度是3m时,最大宽度是6m.
第二方案:
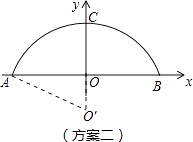
由垂径定理得:圆心O′在y轴上(原点的下方)
设圆的半径是R,在Rt△OAO′中,由勾股定理得:62+(R4)2=R2,
解得R=6.5,
当高度是3m时,最大宽度= ![]() =4
=4 ![]() ≈6.9m
≈6.9m
根据上面的计算得:为了工厂的特种卡车通过厂门更安全,所以采用第二种方案更合理.
【解析】方案一、根据已知中的AB的长,可得出此抛物线与x轴的两交点A、B的坐标,设函数解析式为交点式,再将点C的坐标代入解析式,即可求出函数解析式,然后将y=3代入求出对应的自变量的值,可得出最大宽度为6m;方案二、根据题意可知圆点在y轴的(原点)下方,连接O′A,根据垂径定理求出OA的长,然后在Rt△OAO′中,根据勾股定理建立关于R的方程,求解得出圆的半径长,再根据工厂的运输卡车的高度是3m,求出最大宽度,则宽度较大的设计方案能保工厂的卡车在通过厂门时更安全。
【考点精析】通过灵活运用勾股定理的概念和垂径定理,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧即可以解答此题.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】(1)在下面的括号内,填上推理的依据.
①如图1,![]() ,求证
,求证![]()
证明:![]()
![]() ,
,
![]()
![]() (_____________)
(_____________)
![]() (_____________)
(_____________)
②如图2,![]() ,求证
,求证![]()
证明:![]() ,
,
![]() (_____________)
(_____________)
![]()
![]() (_____________)
(_____________)
![]() (_____________)
(_____________)
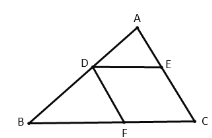
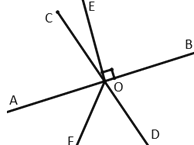
(2)如图,直线![]() 相交于点
相交于点![]() 平分
平分![]() 求①
求①![]() 的度数;②
的度数;②![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
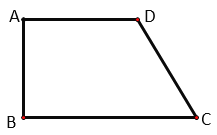
【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣4x+3.
(1)求函数图象的对称轴、顶点坐标、与坐标轴交点的坐标,并画出函数的大致图象;
(2)根据图象直接写出函数值y为负数时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,![]() 的顶点均在格点上.
的顶点均在格点上.
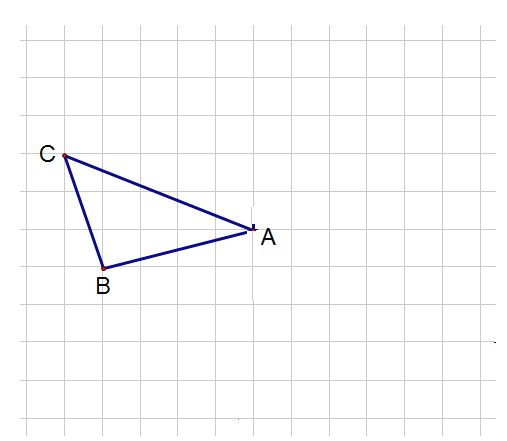
(1)请建立合适的平面直角坐标系,使点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() 和
和![]() ,并写出点
,并写出点![]() 的坐标为___________;
的坐标为___________;
(2)在(1)的条件下.①![]() 中任意一点
中任意一点![]() 经平移后对应点
经平移后对应点![]() ,将
,将![]() 作同样的平移得到
作同样的平移得到![]() ,请画出
,请画出![]() ,并直接写出点
,并直接写出点![]() 的坐标;
的坐标;
②点![]() 在
在![]() 轴上,且
轴上,且![]() ,则点
,则点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,这是某市部分简图,为了确定各建筑物的位置:

(1)请你以火车站为原点建立平面直角坐标系,若以小方格的边长为单位长度,写出市场的坐标为_______;超市的坐标为_____________.
(2)请将体育场为A、宾馆为C和火车站为B看作三点用线段连起来,得△ABC,然后将△ABC向下平移4个单位长度,画出平移后的![]() ,写出
,写出![]() 的坐标.
的坐标.
(3)求出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦BC=4㎝,F是弦BC的中点,∠ABC=60°,若动点E以1 ㎝/s的速度从A点出发在AB上沿着A→B→A运动,设运动时间为t(s)(0≤t<16),连接EF,当△BEF是直角三角形时,t(s)的值为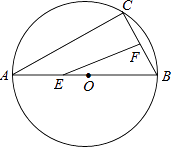
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com